【题目】如图1,在直角坐标系中放入一个边长AB长为3,BC长为5的矩形纸片ABCD,使得BC、AB所在直线分别与x、y轴重合.将纸片沿着折痕AE翻折后,点D恰好落在x轴上,记为F.

(1)求折痕AE所在直线与x轴交点的坐标;
(2)如图2,过D作DG⊥AF,求DG的长度;
(3)将矩形ABCD水平向右移动n个单位,则点B坐标为(n,0),其中n>0.如图3所示,连接OA,若△OAF是等腰三角形,试求点B的坐标.
参考答案:
【答案】(1)折痕AE所在直线与x轴交点的坐标为(9,0);(2)3;(3)点B(4,0)或B(1,0).
【解析】
(1)根据四边形ABCD是矩形以及由折叠对称性得出AF=AD=5,EF=DE,进而求出BF的长,即可得出E点的坐标,进而得出AE所在直线与x轴交点的坐标;
(2)判断出△DAG≌△AFB,即可得出结论;
(3)分三种情况讨论:若AO=AF,OF=FA,AO=OF,利用勾股定理求出即可.
解:(1)∵四边形ABCD是矩形,
∴AD=CB=5,AB=DC=3,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=5,EF=DE,
在Rt△ABF中,BF=![]() =4,
=4,
∴CF=1,
设EC=x,则EF=3﹣x,
在Rt△ECF中,12+x2=(3﹣x)2,
解得:x=![]() ,
,
∴E点坐标为:(5,![]() ),
),
∴设AE所在直线解析式为:y=ax+b,
则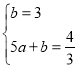 ,
,
解得: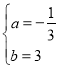 ,
,
∴AE所在直线解析式为:y=![]() x+3,
x+3,
当y=0时,x=9,
故折痕AE所在直线与x轴交点的坐标为:(9,0);
(2)在△DAG和△AFB中
∵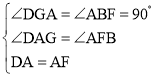 ,
,
∴△DAG≌△AFB,
∴DG=AB=3;
(3)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=4,
∴n=4,
∴B(4,0),
若OF=FA,则n+4=5,
解得:n=1,
∴B(1,0),
若AO=OF,
在Rt△AOB中,AO2=OB2+AB2=m2+9,
∴(n+4)2=n2+9,
解得:n=![]() (n<0不合题意舍去),
(n<0不合题意舍去),
综上所述,若△OAF是等腰三角形,n的值为n=4或1.
即点B(4,0)或B(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
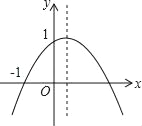
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
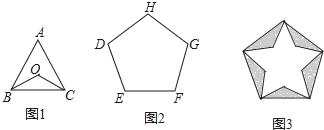
A. 36° B. 42° C. 45° D. 48°
-
科目: 来源: 题型:
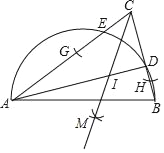
查看答案和解析>>【题目】阅读下面材料:如图,AB是半圆的直径,点D、E在半圆上,且D为弧BE的中点,连接AE、BD并延长,交圆外一点C,按以下步骤作图:
①以点C为圆心,小于BC长为半径画弧,分别交AC、BC于点G、H;
②分别以点G、H为圆心,大于
 GH的长为半径画弧,两弧相交于点M;
GH的长为半径画弧,两弧相交于点M;③作射线CM,交连接A、D两点的线段于点I.
则点I到△ABC各边的距离_____.(填“相等”或“不等”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AD=BE=2,点M,P,N分别是DE,BD,AB的中点,则△PMN的周长=___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
相关试题

