【题目】已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AEDE.
参考答案:
【答案】证明:(1)连接BN,
∵点N为△ABC的内心,
∴∠1=∠2,∠3=∠4.
∴∠BCE=∠1,
∴EB=EC.
∵∠5与∠2都是弧EC所对的圆周角,
∴∠5=∠2=∠1.
∴∠4+∠5=∠3+∠1.
∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,
∴∠NBE=∠BNE.
∴EB=EN.
∴EB=EN=EC.
(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,
∴△BED∽△AEB.
∴![]() .
.
即BE2=AEDE.
∵EB=EN,
∴NE2=AEDE.
【解析】点N为△ABC的内心,易证EB=EC,只需证明EB=EN,或EN=EC,可以通过等角对等边得出;欲证NE2=AEDE,即证BE2=AEDE,可以通过证明△BED∽△AEB得出.
【考点精析】利用三角形的内切圆与内心对题目进行判断即可得到答案,需要熟知三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公共汽车线路收支差额y(万元)与乘客量x(万人)的函数图象(注:收支差额=票价总收入﹣运营成本).目前这条线路亏损,为了扭亏,经市场调研,公交公司决定改革:降低运营成本,同时适当提高票价.则改革后y与x的函数图象可能是( )
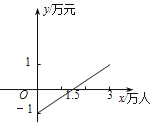
A.
 B.
B. 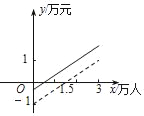
C.
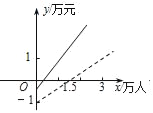 D.
D. 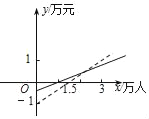
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并填空
问题:在一条直线上有A,B,C,D四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以A为端点的线段有AB,AC,AD 3条,同样以B为端点,以C为端点,以D为端点的线段也各有3条,这样共有4个3,即4×3=12(条),但AB和BA是同一条线段,即每一条线段重复一次,所以一共
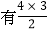 条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.
条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.知识迁移:
如果在一个锐角∠AOB内部画2条射线OC,OD,那么这个图形中总共有____________个角,若在∠AOB内画n 条射线,则总共有___________个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备___________种不同的车票。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲乙两人合作需要8天完成任务,若甲单独做需要12天完成任务.
(1)若甲乙两人一起做6天,剩下的由甲单独做,还需要几天完成?
(2)若甲乙两人一起做4天,剩下的由乙单独做,还需要几天完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4
B.8
C.12
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AB=AC,点M、N在边BC上,且∠MAN=60°.若BM=2,CN=4,则MN的长为_____.
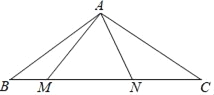
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
A.35°、145°
B.110°、70°
C.55°、125°
D.110°
相关试题

