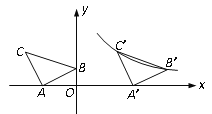
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
(1)点C的坐标是 ;
(2)将△ABC沿x轴正方向平移得到△A′ B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
参考答案:
【答案】(1) (-3, 2) (2)![]()
【解析】试题分析:(1)过C作CN垂直于x轴,交x轴于点N,由A、B及C的坐标得出OA,OB,CN的长,再证明Rt△CNA≌Rt△AOB,由∠CAB=90°,根据全等三角形的对应边相等可得出CN=0A,AN=0B,由AN+OA求出ON的长,再由C在第二象限,可得出点C的坐标;(2)(2)由第一问求出的C与B的横坐标之差为3,根据平移的性质得到纵坐标不变,故设出C′(m,2),则B′(m+3,1),再设出反比例函数解析式,将C′与B′的坐标代入得到关于k与m的两方程,消去k得到关于m的方程,求出方程的解得到m的值,即可确定出k的值,得到反比例函数解析式.
试题解析:
(1) (-3, 2)
(2) 解:设平移距离为a, 则点C′(-3+a,2),点B′(a,1)
∴![]() ,
, ![]() ∴2(-3+a)=a
∴2(-3+a)=a
解得a=6
∴![]() =a=6
=a=6
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了4个单位长度到达点C处,蚂蚁乙从图中点B的位置沿数轴向左爬了8个单位长度到达点D处.

(1)在图中描出点C、D的位置;
(2)点E到点C与点D的距离相等,在数轴上描出点E的位置,并用“<”把点A、B、C、D、E所表示的数连接起来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A、B,与一次函数y2=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D.
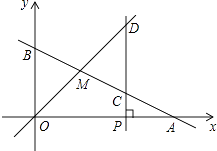
(1)求一次函数y1=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】父亲今年的年龄为51岁,三年后,父亲的年龄是儿子年龄的3倍,则儿子今年的年龄是___岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 一个图形平移后,它各点的横、纵坐标都发生变化
B. 一个图形平移后,它的大小发生变化,形状不变
C. 把一个图形沿y轴平移若干个单位长度后,与原图形相比各点的横坐标没有发生变化
D. 图形平移后,一些点的坐标可以不发生变化
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们做足球操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面的那个同学,这种做法用几何知识解释应是( )
A. 两点之间,线段最短 B. 射线只有一个端点
C. 两点确定一条直线 D. 两直线相交只有一个交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子中,不能成立的是( )
A.﹣(﹣2)=2
B.﹣|﹣2|=﹣2
C.23=6
D.(﹣2)2=4
相关试题

