【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.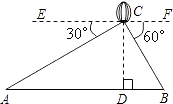
参考答案:
【答案】解:由已知,得∠ECA=30°,∠FCB=60°,CD=90,
EF∥AB,CD⊥AB于点D.
∴∠A=∠ECA=30°,∠B=∠FCB=60°.
在Rt△ACD中,∠CDA=90°,tanA= ![]() ,
,
∴AD= ![]() =90×
=90× ![]() =90
=90 ![]() .
.
在Rt△BCD中,∠CDB=90°,tanB= ![]() ,
,
∴DB= ![]() =30
=30 ![]() .
.
∴AB=AD+BD=90 ![]() +30
+30 ![]() =120
=120 ![]() .
.
答:建筑物A、B间的距离为120 ![]() 米
米
【解析】添加辅助线,将相关的问题转化到直角三角形中求解。过点C作CD⊥AB于点D,根据已知易求得∠A、∠B的度数,再在Rt△ACD和Rt△BCD中,分别求出DB、AD的长,就可以求出AB的长。
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法),以及对关于仰角俯角问题的理解,了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为 a,宽为 b 的长方形.现将相等的长方形若干,拼接组成如下图 形.
(1)将图①中所得的四块长为 a,宽为 b 的小长方形拼成一个正方形(如图②).请利用 图②中阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a﹣b)2、ab 之间的等量关系是 ;
(2)根据(2)题中的等量关系,解决如下问题:已知 m+n=6,mn=5,则 m﹣n= ;
(3)将图①中的长方形和图③中的两个边长分别为 a、b 的正方形若干个,拼成如图④的长方形,则图④中的长方形的面积可以用两种不同的方法表示,则关系式 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:

请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E,F分别在矩形ABCD的边BC和CD上.
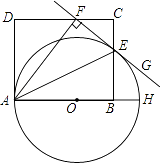
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.
相关试题

