【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.
参考答案:
【答案】
(1)解:∵抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3
(2)解:如图1,
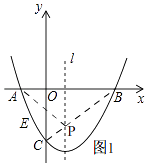
∵点A,B关于直线l对称,
∴连接BC交直线l于点P,
由(1)知,抛物线的解析式为y=x2﹣2x﹣3,
∴直线l:x=1,C(0,﹣3),
∵B(3,0),
∴直线BC的解析式为y=x﹣3,
当x=1时,y=﹣2,
∴P(1,﹣2)
(3)解:设点M(1,m),
∵A(﹣1,0),C(0,﹣3),
∴AC2=10,AM2=m2+4,CM2=(m+3)2+1=m2+6m+10,
∵△MAC为直角三角形,
∴当∠ACM=90°时,∴AC2+CM2=AM2,
∴10+m2+6m+10=m2+4,
∴m=﹣ ![]() ,
,
∴M(1,﹣ ![]() )
)
当∠CAM=90°时,∴AC2+AM2=CM2,
∴10+m2+4=m2+6m+10,
∴m= ![]() ,
,
∴M(1, ![]() )
)
当∠AMC=90°时,AM2+CM2=AC2,
∴m2+4+m2+6m+10=10,
∴m=﹣1或m=﹣2,
∴M(1,﹣1)或(1,﹣2),
即:满足条件的点M的坐标为(1,﹣ ![]() )或(1,
)或(1, ![]() )或(1,﹣1)或(1,﹣2)
)或(1,﹣1)或(1,﹣2)
【解析】(1)方法一、将A、B两点坐标代入函数解析式即可求。方法二、A、B两点是抛物线与x轴的交点坐标,a=1可设抛物线解析式为y=(x+1)(x-3).
(2)由题意可知点A,B关于直线l对称,连接BC交直线l于点P,求出直线BC的函数解析式,即可求出点P的坐标。
(3)由于点M也是直线l上的动点,△MAC为直角三角形,因此设点M(1,m),根据A、C两点坐标,分别求出AC2、AM2、CM2。再分三种情况:当∠ACM=90°时,∴AC2+CM2=AM2,当∠CAM=90°时,∴AC2+AM2=CM2,当∠AMC=90°时,AM2+CM2=AC2,分别建立方程,求出m的值,即可求得点m的坐标。
【考点精析】本题主要考查了确定一次函数的表达式和轴对称-最短路线问题的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.
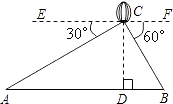
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E,F分别在矩形ABCD的边BC和CD上.
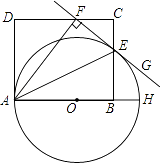
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中,既是轴对称图形又是中心对称图形的个数为( )
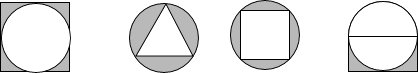
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
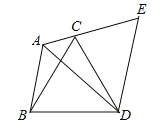
查看答案和解析>>【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
-
科目: 来源: 题型:
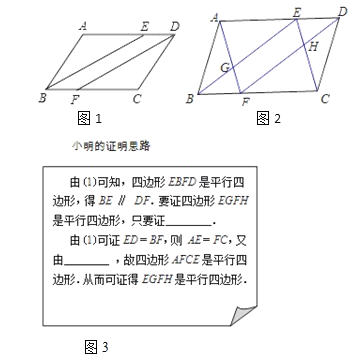
查看答案和解析>>【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
相关试题

