【题目】若关于t的不等式组 ![]() ,恰有三个整数解,则关于x的一次函数
,恰有三个整数解,则关于x的一次函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]() 的图象的公共点的个数为 .
的图象的公共点的个数为 .
参考答案:
【答案】1或0
【解析】解:不等式组的解为:a≤t≤ ![]() , ∵不等式组恰有3个整数解,
, ∵不等式组恰有3个整数解,
∴﹣2<a≤﹣1.
联立方程组 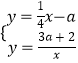 ,
,
得: ![]() x2﹣ax﹣3a﹣2=0,
x2﹣ax﹣3a﹣2=0,
△=a2+3a+2=(a+ ![]() )2﹣
)2﹣ ![]() =(a+1)(a+2)
=(a+1)(a+2)
这是一个二次函数,开口向上,与x轴交点为(﹣2,0)和(﹣1,0),对称轴为直线a=﹣ ![]() ,
,
其图象如下图所示: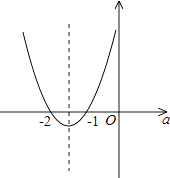
由图象可见:
当a=﹣1时,△=0,此时一元二次方程有两个相等的根,即一次函数与反比例函数有一个交点;
当﹣2<a<﹣1时,△<0,此时一元二次方程无实数根,即一次函数与反比例函数没有交点.
∴交点的个数为:1或0.
所以答案是:1或0.
【考点精析】本题主要考查了一元一次不等式组的整数解的相关知识点,需要掌握使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013成都)若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片 ABCD 折叠,AE、EF 为折痕,点 C 落在 AD 边上的 G 处, 并且点 B 落在 EG 边的 H 处,若 AB=
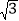 ,∠BAE=30°,则 BC 边的长为( )
,∠BAE=30°,则 BC 边的长为( )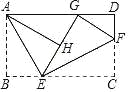
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=
 x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=-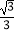 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 .
.
其中正确的是 . (写出所有正确说法的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C为⊙O上相邻的三个n等分点,
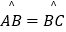 ,点E在
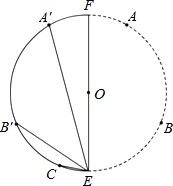
,点E在 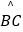 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= 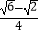 ,cos15°=sin75°=
,cos15°=sin75°= 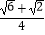 )
)
相关试题

