【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= ![]() x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=- ![]() 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 ![]() .
.
其中正确的是 . (写出所有正确说法的序号)
参考答案:
【答案】③④
【解析】解:设A(m,km),B(n,kn),其中m<0,n>0.
联立y= ![]() x2﹣2与y=kx得:
x2﹣2与y=kx得: ![]() x2﹣2=kx,即x2﹣3kx﹣6=0,
x2﹣2=kx,即x2﹣3kx﹣6=0,
∴m+n=3k,mn=﹣6.
设直线PA的解析式为y=ax+b,将P(0,﹣4),A(m,km)代入得:![]() ,解得a=
,解得a= ![]() ,b=﹣4,
,b=﹣4,
∴y=( ![]() )x﹣4.
)x﹣4.
令y=0,得x= ![]() ,
,
∴直线PA与x轴的交点坐标为( ![]() ,0).
,0).
同理可得,直线PB的解析式为y=( ![]() )x﹣4,直线PB与x轴交点坐标为(
)x﹣4,直线PB与x轴交点坐标为( ![]() ,0).
,0).
∵ ![]() +
+ ![]() =
= ![]() =
= ![]() =0,
=0,
∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
1)说法①错误.理由如下:
如答图1所示,∵PA、PB关于y轴对称,
∴点A关于y轴的对称点A′落在PB上.
连接OA′,则OA=OA′,∠POA=∠POA′.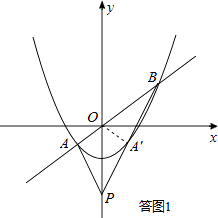
假设结论:PO2=PAPB成立,即PO2=PA′PB,
∴ ![]() ,
,
又∵∠BPO=∠BPO,
∴△POA′∽△PBO,
∴∠POA′=∠PBO,
∴∠AOP=∠PBO.
而∠AOP是△PBO的外角,
∴∠AOP>∠PBO,矛盾,
∴说法①错误.
2)说法②错误.理由如下:
易知: ![]() =﹣
=﹣ ![]() ,
,
∴OB=﹣ ![]() OA.
OA.
由对称可知,PO为△APB的角平分线,
∴ ![]() ,
,
∴PB=﹣ ![]() PA.
PA.
∴(PA+AO)(PB﹣BO)=(PA+AO)[﹣ ![]() PA﹣(﹣
PA﹣(﹣ ![]() OA)]=﹣
OA)]=﹣ ![]() (PA+AO)(PA﹣OA)=﹣
(PA+AO)(PA﹣OA)=﹣ ![]() (PA2﹣AO2).
(PA2﹣AO2).
如答图2所示,过点A作AD⊥y轴于点D,则OD=﹣km,PD=4+km.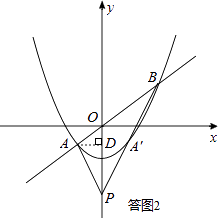
∴PA2﹣AO2=(PD2+AD2)﹣(OD2+AD2)=PD2﹣OD2=(4+km)2﹣(﹣km)2=8km+16,
∵m+n=3k,∴k= ![]() (m+n),
(m+n),
∴PA2﹣AO2=8 ![]() (m+n)m+16=
(m+n)m+16= ![]() m2+
m2+ ![]() mn+16=
mn+16= ![]() m2+
m2+ ![]() ×(﹣6)+16=
×(﹣6)+16= ![]() m2 .
m2 .
∴(PA+AO)(PB﹣BO)=﹣ ![]() (PA2﹣AO2)=﹣
(PA2﹣AO2)=﹣ ![]()
![]() m2=﹣
m2=﹣ ![]() mn=﹣
mn=﹣ ![]() ×(﹣6)=16.
×(﹣6)=16.
即:(PA+AO)(PB﹣BO)为定值,所以说法②错误.
3)说法③正确.理由如下:
当k= ![]() 时,联立方程组:
时,联立方程组:  ,得A(
,得A( ![]() ,2),B(
,2),B( ![]() ,﹣1),
,﹣1),
∴BP2=12,BOBA=2×6=12,
∴BP2=BOBA,故说法③正确.
4)说法④正确.理由如下:
S△PAB=S△PAO+S△PBO= ![]() OP(﹣m)+
OP(﹣m)+ ![]() OPn=
OPn= ![]() OP(n﹣m)=2(n﹣m)=2
OP(n﹣m)=2(n﹣m)=2 ![]() =2
=2 ![]() ,
,
∴当k=0时,△PAB面积有最小值,最小值为 ![]() =
= ![]() .
.
故说法④正确.
综上所述,正确的说法是:③④.
所以答案是:③④.
【考点精析】本题主要考查了根与系数的关系的相关知识点,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于t的不等式组
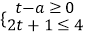 ,恰有三个整数解,则关于x的一次函数
,恰有三个整数解,则关于x的一次函数 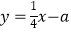 的图象与反比例函数
的图象与反比例函数 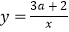 的图象的公共点的个数为 .
的图象的公共点的个数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

-
科目: 来源: 题型:
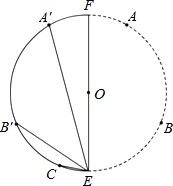
查看答案和解析>>【题目】如图,A,B,C为⊙O上相邻的三个n等分点,
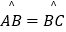 ,点E在
,点E在 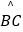 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= 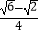 ,cos15°=sin75°=
,cos15°=sin75°= 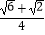 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
造型花卉
甲
乙
A
80
40
B
50
70
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

相关试题

