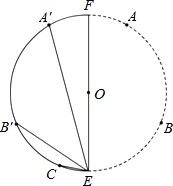
【题目】如图,A,B,C为⊙O上相邻的三个n等分点, ![]() ,点E在
,点E在 ![]() 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= ![]() ,cos15°=sin75°=
,cos15°=sin75°= ![]() )
)
参考答案:
【答案】c+ ![]() b;c+
b;c+ ![]() b
b
【解析】解:如解答图所示,连接AB、AC、BC. 由题意,点A、B、C为圆上的n等分点,
∴AB=BC,∠ACB= ![]() ×
× ![]() =
= ![]() (度).
(度).
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BCcos∠ACB=2cos ![]() BC,
BC,
∴ ![]() =2cos
=2cos ![]() .
.
连接AE、BE,在AE上取一点D,使ED=EC,连接CD.
∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形,
∴△ABC∽△CED.
∴ ![]() ,∠ACB=∠DCE.
,∠ACB=∠DCE.
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵ ![]() ,∠ACD=∠BCE,
,∠ACD=∠BCE,
∴△ACD∽△BCE.
∴ ![]() ,
,
∴DA= ![]() EB=2cos
EB=2cos ![]() EB.
EB.
∴EA=ED+DA=EC+2cos ![]() EB.
EB.
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC.
∴p=c+2cos ![]() b.
b.
当n=4时,p=c+2cos45°b=c+ ![]() b;
b;
当n=12时,p=c+2cos15°b=c+ ![]() b.
b.
所以答案是:c+ ![]() b,c+
b,c+ ![]() b.
b.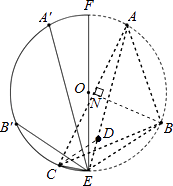
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于t的不等式组
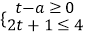 ,恰有三个整数解,则关于x的一次函数
,恰有三个整数解,则关于x的一次函数 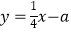 的图象与反比例函数
的图象与反比例函数 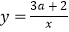 的图象的公共点的个数为 .
的图象的公共点的个数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=
 x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=-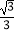 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 .
.
其中正确的是 . (写出所有正确说法的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
造型花卉
甲
乙
A
80
40
B
50
70
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

-
科目: 来源: 题型:
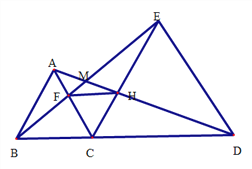
查看答案和解析>>【题目】如图,已知△ABC和△ECD都是等边三角形, B、C、D在一条直线上。
求证:(1)BE=AD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD;
(5)求∠EMD的度数。;
相关试题

