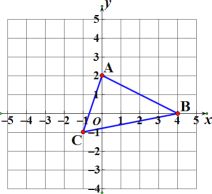
【题目】如图，在边长为 1 的正方形网格中，三角形 ABC 中任意一点 P(x0，y0)经平移后对应点为 P1(x0-4，y0＋3)，已知 A(0，2)，B(4，0)，C(-1，-1)，将三角形 ABC 作同样的平移得到三角形 A1B1C1

(1)直接写出坐标：A1( ， )，B1( ， )，C1( ， )；

(2)三角形 A1B1C1 的面积为 ；

(3)已知点 P 在 y 轴上，且三角形 PAC 的面积等于三角形 ABC 面积的一半，求 P 点坐标．

参考答案：

【答案】（1）-4，5，0，3，-5，2；（2）7；（3）P(0，9)或P(0，-5)．

【解析】

（1）由点P的对应点P1坐标知，需将三角形向左平移4个单位、向上平移3个单位，据此可得；

（2）直接利用割补法求出△A1B1C1的面积即可；

（3）△PAC以PA为底时，高为C点到y轴的距离，据此可得，再根据三角形 PAC 的面积等于三角形 ABC 面积的一半即可求出PA的长度，由此可求得P点坐标．

解：（1）0-4=-4,2+3=5，则A1 (-4，5)，

4-4=0,0+3=3，则B1（0，3），

-1-4=-5，-1+3=2，则C1(-5，2）；

故答案为：-4，5，0，3，-5，2；

（2）如下图，

，

故答案为：7；

（3），

∴，

又∵A(0，2)，

∴P(0，9)或P(0，-5)．

关闭