Question

【题目】如图,直线l1 :y=-3x+3与x轴交于点D，直线l2经过A(4,0)、B(3,)两点，直线l1 与直线l2交于点C.

(1)求直线l2的解析式和点C的坐标；

(2)在 y轴上是否存在一点P，使得四边形PDBC的周长最小？若存在，请求出点P的坐标，若不存在，请说明理由.

Answer 1

【答案】(1) y=x-6，点C(2,-3)；(2)存在，点P的坐标为(0,-1).

【解析】

（1）将点A(4,0)、B(3，-)代入y=kx+b中，用待定系数法即可求出直线l2的解析式；联立两直线的解析式即可求出点C的坐标；

（2）作点D关于y轴的对称点D1，连结C D1，交y轴于一点，则该点即为要求的点P，用待定系数法求出CD1的解析式，然后可求出点P的坐标.

(1) 设直线l2的解析式为y=kx+b(k≠0)，将点A(4,0)、B(3，-)代入y=kx+b中，

，

解得 ，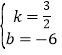

所以直线l2的解析式为y=x-6.

联立方程组，

，

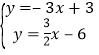解得，

∴点C(2,-3) ；

(2)存在，作点D关于y轴的对称点D1，连结C D1，交y轴于一点，则该点即为要求的点P，

在y=-3x+3中，令y=0，则x=1，即点D(1,0)，点D关于y轴的对称点D1(-1,0)，

∴点C(,0).

设直线C D1的解析式为y=kx+b(k≠0)，将点C(2,-3)、D1(-1,0)代入，得：

得：，解得

∴直线BC的解析式为y=-x-1 ，令x=0，则y=-1，

则点P的坐标为(0,-1).