【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过坐标原点
经过坐标原点![]() ,与抛物线的一个交点为
,与抛物线的一个交点为![]() ,与抛物线的对称交于点
,与抛物线的对称交于点![]() ,连接
,连接![]() ,点
,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
(![]() )求抛物线的解析式,并分别求出点
)求抛物线的解析式,并分别求出点![]() 和点
和点![]() 的坐标.
的坐标.
(![]() )在抛物线上是否存在点
)在抛物线上是否存在点![]() ,使
,使![]() ≌
≌![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:(1)利用待定系数法求抛物线的函数表达式和直线DE的解析式,利用配方法求抛物线的对称轴,即点E的横坐标为x=3,代入直线DE中可求得E的纵坐标,根据对称性求得点B的坐标;
(2)如图,根据△FOE≌△FCE,对应边相等,得FC=FO,所以F在OC的中垂线上,点F纵坐标为-4,代入抛物线后求得点F的坐标
试题解析:(![]() )∵抛物线
)∵抛物线![]() 经过点
经过点![]() ,
, ![]() ,
,
∴![]() ,计算得出
,计算得出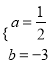 ,
,
∴抛物线的函数表达式![]() ,
,
∵![]() ,
,
∴抛物线的对称轴为直线![]() .
.
又抛物线与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
∴点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() .
.
∵点![]() ,计算得出
,计算得出![]() ,
,
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∵点![]() 为直线
为直线![]() 和抛物线对称轴的交点,
和抛物线对称轴的交点,
∴点![]() 的横坐标为
的横坐标为![]() ,纵坐标不
,纵坐标不![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(![]() )抛物线上存在点
)抛物线上存在点![]() ,使
,使![]() ≌
≌![]() .
.
∵![]() ,
,
∴![]() ,
,
∴点![]() 在
在![]() 的垂直平分线上,此时点
的垂直平分线上,此时点![]() 的纵坐标为
的纵坐标为![]() .
.
∴![]() ,计算得出
,计算得出![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10a3-3a2b+2a)÷a=__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计(设每天的诵读时间为
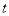 分钟),将调查统计的结果分为四个等级:Ⅰ级
分钟),将调查统计的结果分为四个等级:Ⅰ级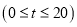 、Ⅱ级
、Ⅱ级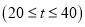 、Ⅲ级
、Ⅲ级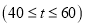 、Ⅳ级
、Ⅳ级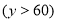 .将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: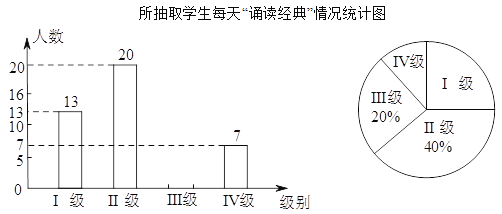
(
 )请补全上面的条形图.
)请补全上面的条形图.(
 )所抽查学生“诵读经典”时间的中位数落在__________级.
)所抽查学生“诵读经典”时间的中位数落在__________级.(
 )如果该校共有
)如果该校共有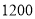 名学生,请你估计该校平均每天“诵读经典”的时间不低于
名学生,请你估计该校平均每天“诵读经典”的时间不低于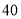 分钟的学生约有多少人?
分钟的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
解:我写的真命题是:
在△ABC和△DEF中,如果 ,那么 .(不能只填序号)
证明如下:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文印店,一次性复印收费
 (元)与复印面数(8开纸)
(元)与复印面数(8开纸)  (面)的函数关系如图所示:
(面)的函数关系如图所示:(1)从图象中可看出:复印超过50面的部分每面收费 元,复印200面平均每面收费 元;
(2)两同学各需要复印都不多于50面的资料,他们合起来去该店复印,结果比各自独去复印两人共节省2元钱,问其中一位同学所需复印的面数不能少于多少面?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果xny4与2xym相乘的结果是2x5y7,那么m=______,n=_______
相关试题

