【题目】如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B、C、E三点在同一条直线上.
),且B、C、E三点在同一条直线上. 
(1)求斜坡AC的长;
(2)请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
参考答案:
【答案】
(1)解:如图,过点A作AF⊥DE于F,
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3米,
设DE=x,
在Rt△CDE中,CE= ![]() =
= ![]() x,
x,
在Rt△ABC中,
∵ ![]() =
= ![]() ,AB=3,
,AB=3,
∴BC=3 ![]() ,
,
AC= ![]() =
= ![]() =6(米)\
=6(米)\

(2)解:在Rt△AFD中,DF=DE﹣EF=x﹣3,
∴AF= ![]() =
= ![]() (x﹣3),
(x﹣3),
∵AF=BE=BC+CE,
∴ ![]() (x﹣3)=3
(x﹣3)=3 ![]() +
+ ![]() x,
x,
解得x=9.
答:树高为9米
【解析】过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2(y6)2-(y4)3; (2)(ab2c)2÷(ab3c2);
(3)(-x-y)(x-y)+(x+y)2 (4)利用公式计算803×797;
(5)计算:
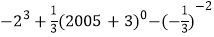
-
科目: 来源: 题型:
查看答案和解析>>【题目】人民公园划出一块矩形区域,用以栽植鲜花.
(1)经测量,该矩形区域的周长是72m,面积为320m2 , 请求出该区域的长与宽;
(2)公园管理处曾设想使矩形的周长和面积分别为(1)中区域的周长和面积的一半,你认为此设想合理吗?如果此设想合理,请求出其长和宽;如果不合理,请说明理由,并求出在(1)中周长减半的条件下矩形面积的最大值.
-
科目: 来源: 题型:
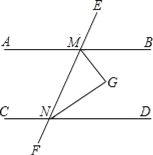
查看答案和解析>>【题目】如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=
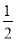 ∠BMN
∠BMN 同理∠GNM=
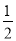 ∠DNM.
∠DNM.∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
-
科目: 来源: 题型:
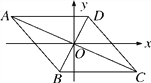
查看答案和解析>>【题目】如图,已知点A(-4,2),B(-1,-2),□ABCD的对角线交于坐标原点O.
(1)请写出点C,D的坐标;
(2)指出从线段AB到线段DC的变换过程;
(3)求□ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
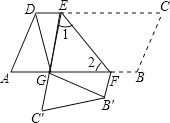
求证:(1)∠1=∠2;
(2)DG=B′G.
相关试题

