【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

参考答案:
【答案】(1)85;85;80;(2)A校成绩好些;(3)A校代表队选手成绩较为稳定.
【解析】
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出A校、B校的方差即可.
解:(1)A校平均数为:![]() (75+80+85+85+100)=85(分),众数85(分);
(75+80+85+85+100)=85(分),众数85(分);
B校中位数80(分).
填表如下:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | 85 | 85 | 85 |
B校 | 85 | 80 | 100 |
故答案为:85;85;80.
(2)A校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些.
(3)∵A校的方差
s12=![]() [(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
B校的方差
s22=![]() [(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.
[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.
∴s12<s22,
因此,A校代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )

A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁 -
科目: 来源: 题型:
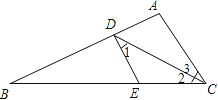
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程的变形正确的是( )
A.由2x﹣3=4x,得:2x=4x﹣3
B.由7x﹣4=3﹣2x,得:7x+2x=3﹣4
C.由 x﹣
x﹣  =3x+4得﹣
=3x+4得﹣  ﹣4=3x+
﹣4=3x+  x
x
D.由3x﹣4=7x+5得:3x﹣7x=5+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若
 ,求m、n的值.
,求m、n的值.解:∵
 ,
,∴
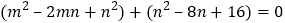
∴
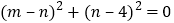 ,而
,而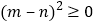 ,
,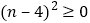 ,
, ∴
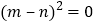 且
且 ,
,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)
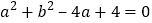 ,则a=______;b=_________.
,则a=______;b=_________.(2)已知△ABC的三边a,b,c满足
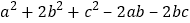 =0,
=0,关于此三角形的形状的以下命题:①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.其中所有正确命题的序号为________________.
(3)已知△ABC的三边长a、b、c都是正整数,且
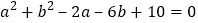 ,求△ABC的周长.
,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

-
科目: 来源: 题型:
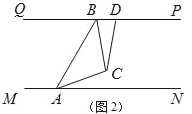
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

相关试题

