【题目】太阳山中学九年级举行跳绳比赛,要求每班选出![]() 名学生参加,在规定时间内每人跳绳不低于
名学生参加,在规定时间内每人跳绳不低于![]() 次为优秀,冠、亚军会在甲、乙两班中产生,下表是这两个班的5名学生的比赛数据(单位:次)
次为优秀,冠、亚军会在甲、乙两班中产生,下表是这两个班的5名学生的比赛数据(单位:次)
|
|
|
|
| 平均次数 | 方差 | |
甲班 |
|
|
|
|
|
|
|
乙班 |
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)求出表中![]() 的值和甲、乙两班比赛学生的优秀率;
的值和甲、乙两班比赛学生的优秀率;
(2)求出两班的跳绳比赛数据的中位数;
(3)请你结合表格和自己所算出的数据判断冠军应发给哪个班?简要说明理由.
参考答案:
【答案】(1)150,40%,20%;(2)153,147 ;(3)见解析
【解析】
(1)根据平均数,优秀率的概念,即可求解;
(2)根据中位数的定义,即可求解;
(3)分别从优秀率,中位数和方差的角度,对甲乙班数据进行分析,即可得到结论.
(1)由题意得:a=(139+150+145+169+147)÷5=150,
甲班的优秀率=3÷5×100%=60%,
乙班的优秀率=2÷5×100%=40%;
(2)把甲班的数据从小到大排列为:139,148,150,153,160,
∴甲班的中位数是150次,
把乙班的数据从小到大排列为:139,145,147,150,169,
∴乙班的中位数是147次;
(3)冠军奖应发给甲班,
因为甲的优秀率高于乙,说明甲的优秀人数多,甲的中位数大于乙的中位数,说明甲的一般水平高,甲的方差小于乙的方差,说明甲比较稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
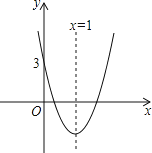
A. ②③④B. ①②③C. ②③D. ①④
-
科目: 来源: 题型:
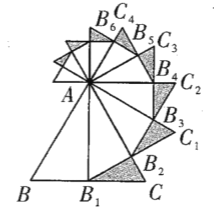
查看答案和解析>>【题目】如图,已知等边
 的边长是
的边长是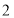 ,以
,以 边上的高
边上的高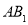 ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边 ;再以等边
;再以等边 的
的 边上的高
边上的高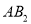 ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边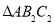 ,再以等边
,再以等边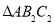 的
的 边上的高
边上的高 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边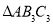 : ....记
: ....记 的面积为
的面积为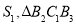 的面积为
的面积为 的面积为
的面积为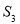 ,如此下去,则
,如此下去,则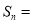 ___________
___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,一架长
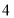 米的梯子
米的梯子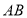 斜靠在与地面
斜靠在与地面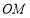 垂直的墙壁
垂直的墙壁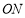 上,梯子与地面所成的角
上,梯子与地面所成的角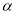 为
为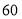 度.
度.(1)求图(1)中的
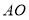 与
与 的长度;
的长度;(2)若梯子顶端
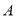 沿
沿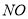 下滑,同时底端
下滑,同时底端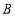 沿
沿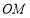 向右滑行.
向右滑行.①如图(2)所示,设
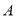 点下滑到
点下滑到 点,
点,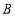 点向右滑行到
点向右滑行到 点,并且
点,并且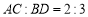 ,请计算
,请计算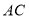 的长度;
的长度;②如图(3)所示,当
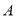 点下滑到
点下滑到 ,
,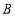 点向右滑行到
点向右滑行到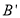 点时,梯子
点时,梯子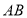 的中点
的中点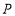 也随之运动到
也随之运动到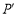 点,若
点,若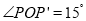 ,试求
,试求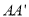 的长度.
的长度.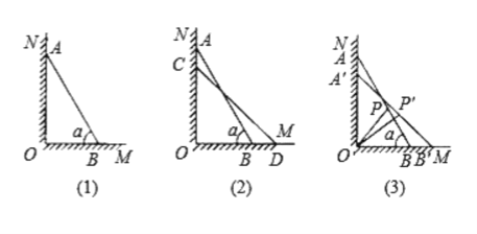
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
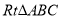 的直角边
的直角边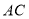 为直径作
为直径作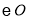 交斜边
交斜边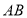 于点
于点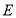 ,连接
,连接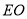 并延长交
并延长交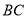 的延长线于点
的延长线于点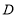 ,作
,作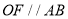 交
交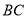 于点
于点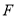 ,连接
,连接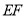 .
.(1)求证:
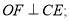
(2)求证:
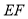 是
是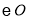 的切线;
的切线;(3)若
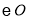 的半径为
的半径为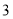 ,
,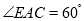 ,求
,求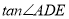 的值.
的值.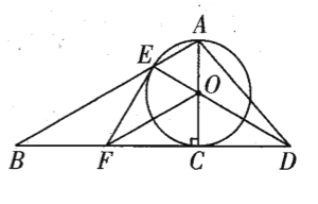
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量
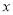 ,这两个函数对应的函数值记为
,这两个函数对应的函数值记为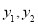 , 恒有点
, 恒有点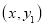 和点
和点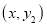 关于点
关于点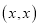 成中心对称(此三个点可以重合),由于对称中心
成中心对称(此三个点可以重合),由于对称中心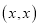 都在直线
都在直线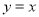 上,所以称这两个函数为关于直线
上,所以称这两个函数为关于直线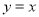 的“相依函数”。例如:
的“相依函数”。例如: 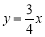 和
和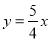 为关于直线
为关于直线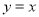 的 “相依函数”.
的 “相依函数”.(1)已知点
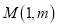 是直线
是直线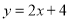 上一点,请求出点
上一点,请求出点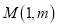 关于点
关于点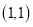 成中心对称的点
成中心对称的点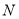 的坐标:
的坐标:(2)若直线
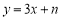 和它关于直线
和它关于直线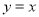 的“相依函数”的图象与
的“相依函数”的图象与 轴围成的三角形的面积为
轴围成的三角形的面积为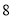 ,求
,求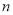 的值;
的值;(3)若二次函数
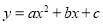 和
和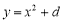 为关于直线
为关于直线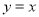 的“相依函数”.
的“相依函数”.①请求出
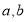 的值;
的值;②已知点
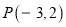 、点
、点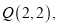 连接
连接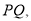 直接写出
直接写出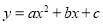 和
和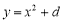 两条抛物线与线段
两条抛物线与线段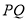 有目只有两个交占时对应的
有目只有两个交占时对应的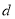 的取值范围.
的取值范围.
相关试题

