【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
参考答案:
【答案】解:
|
|
| |||
| |||||
![]()
![]() 开始
开始
![]()
![]() …………………………(4分)
…………………………(4分)
|
|
| 4 | 5 | |
1 | 1+3=4 | 1+4=5 | 1+5=6 |
2 | 2+3=5 | 2+4=6 | 2+5=7 |
【错一个扣1分,最多扣四分】
![]() …………………………(5分)
…………………………(5分)
![]() …………………………(6分)
…………………………(6分)
![]() 这个方法公平合理。…………………………(7分)
这个方法公平合理。…………………………(7分)
【解析】根据题意列表(或画树状图)如下:
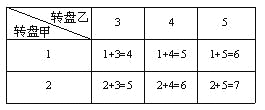
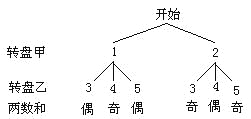
由列表(或树状图)可知:![]() ,
,![]() .
.
所以这个方法是公平的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣ x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行直线上各有
 个点,用这
个点,用这 对点按如下的规则连接线段:①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;②符合①要求的线段必须全部画出;图1展示了当
对点按如下的规则连接线段:①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;②符合①要求的线段必须全部画出;图1展示了当 时的情况,此时图中三角形的个数为0;图2展示了当
时的情况,此时图中三角形的个数为0;图2展示了当 时的一种情况,此时图中三角形的个数为2;图3展示了当
时的一种情况,此时图中三角形的个数为2;图3展示了当 时的一种情况,此时图中三角形的个数为4;试猜想当
时的一种情况,此时图中三角形的个数为4;试猜想当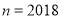 时,按照上述规则画出的图形中,三角形最少有____个
时,按照上述规则画出的图形中,三角形最少有____个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举办了“创建文明城市知识”竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1590元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上
 点、
点、 点表示的数为
点表示的数为 、
、 ,则
,则 、
、 两点之间的距离
两点之间的距离 ;线段
;线段 的中点
的中点 表示的数为
表示的数为 .已知数轴上有
.已知数轴上有 、
、 两点,分别表示的数为
两点,分别表示的数为 和
和 ,点
,点 以每秒
以每秒 个单位的速度沿数轴向右匀速运动,点
个单位的速度沿数轴向右匀速运动,点 以每秒
以每秒 个单位向左匀速运动.设运动时间为
个单位向左匀速运动.设运动时间为 秒(
秒( )
)(
 )运动开始前,
)运动开始前, 、
、 两点的距离为__________;线段
两点的距离为__________;线段 的中点
的中点 所表示的数为__________.
所表示的数为__________.(
 )它们按上述方式运动,
)它们按上述方式运动, 、
、 两点两点经过多少秒会相遇,相遇点所表示的数是什么?
两点两点经过多少秒会相遇,相遇点所表示的数是什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
相关试题

