【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
参考答案:
【答案】(1)14000元;(2)30元
【解析】试题分析:
(1)由题意可知,每箱降价20元时,每箱利润为:(120-20)元,销售量为(100+20×2)箱,两者相乘可得每天获利总额;
(2)这每箱应降价![]() 元,则此时每箱获利为(120-
元,则此时每箱获利为(120- ![]() )元,销售量为(100+
)元,销售量为(100+![]() )箱,由二者相乘等于总利润14400可列方程,解方程求得
)箱,由二者相乘等于总利润14400可列方程,解方程求得![]() ,再结合“每箱获利大于80元”进行检验可得结果.
,再结合“每箱获利大于80元”进行检验可得结果.
试题解析:
(1)当每箱降价20元时,由题意可得此时每天可获利润为:
(120-20)×(100+2×20)=14000(元).
(2)要使每天销售饮料获利14400元,每箱应降价![]() 元,依据题意列方程得:
元,依据题意列方程得:
![]()
整理得: ![]() ,
,
解得: ![]() ,
,
∵ 要求每箱饮料获利大于80元,
∴ ![]() .
.
答:每箱应降价30元,可使每天销售饮料获利14400元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线AC 、BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=
 ,求菱形ABCD的面积.
,求菱形ABCD的面积.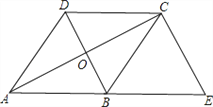
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?
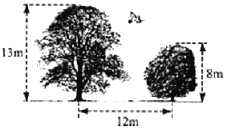
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有( )
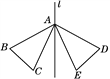
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A. 在AC、BC两边高线的交点处
B. 在AC、BC两边中线的交点处
C. 在AC、BC两边垂直平分线的交点处
D. 在∠A、∠B两内角平分线的交点处
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少
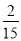 m%.结果10月份利润达到3388元,求m的值(m>10).
m%.结果10月份利润达到3388元,求m的值(m>10). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=
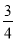 x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.
相关试题

