搜索
【题目】如图，菱形ABCD的对角线AC=3cm，把它沿对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形ENCM的面积之比为（ ）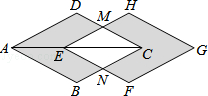 
A.9：4
B.12：5
C.3：1
D.5：2
参考答案：
【答案】D
【解析】解：∵ME∥AD， ∴△MEC∽△DAC，
∴ 
= 
，
∵菱形ABCD的对角线AC=3cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，
∴AE=1cm，EC=2cm，
∴ = 
，
∴ 
= 
，
∴图中阴影部分图形的面积与四边形EMCN的面积之比为： 
= 
．
故选D．
【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半，以及对平移的性质的理解，了解①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等．
-
科目： 来源： 题型：
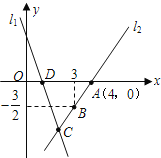
查看答案和解析>>【题目】（本题满分12分）如图，直线l1的解析表达式为：
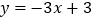，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
【1】（1）求直线l2的函数关系式；
【2】（2）求△ADC的面积；
【3】（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列等式：
第1个等式：a1=
=
﹣
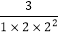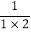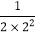；第2个等式：a2=
=﹣
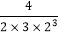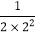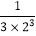；第3个等式：a3=
=﹣
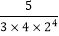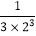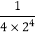；第4个等式：a4=
=﹣
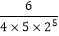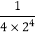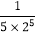．按上述规律，回答以下问题：
（1）用含n的代数式表示第n个等式：an=_____=_____；
（2）式子a1+a2+a3+…+a20=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC，CD，DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则△ABC的面积是 （ ）
A. 10B. 16C. 18D. 20
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着我国的发展与强大，中国文化与世界各国文化的交流与融合进一步加强．为了增进世界各国人民对中国语言和文化的理解，在世界各国建立孔子学院，推广汉语，传播中华文化．同时，各国学校之间的交流活动也逐年增加．在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图，那么“礼”字对面的字是（ ）
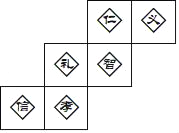
A. 仁 B. 义 C. 智 D. 信
-
科目： 来源： 题型：
查看答案和解析>>【题目】填空，完成下列说理过程
如图，点A，O，B在同一条直线上，OD，OE分别平分∠AOC和∠BOC．求∠DOE的度数．
解：因为OD是∠AOC的平分线，
所以∠COD=
∠AOC． 因为OE是∠BOC 的平分线，
所以 =
∠BOC．所以∠DOE=∠COD+∠COE=
（∠AOC+∠BOC）=∠AOB= °．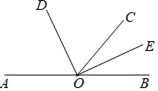
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=x2+bx的图象如图，对称轴为直线x=1，若关于x的一元二次方程x2+bx﹣t=0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是（ ）
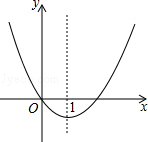
A.t≥﹣1
B.﹣1≤t＜3
C.﹣1≤t＜8
D.3＜t＜8
相关试题
