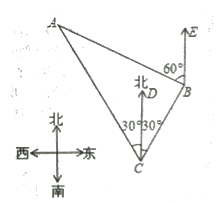
【题目】(10分)如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中![]() 1.732)
1.732)
参考答案:
【答案】此时渔政船距钓鱼岛A的距离AB约为69.3海里.
【解析】试题分析:此题可先由速度和时间求出BC的距离,再由各方向角关系确定△ABC为直角三角形,解此直角三角形即可求得结果.
试题解析:由题意得,BC=80×![]() =40(海里),
=40(海里),
∠ACB=60°,∠DCB=30°,∠EBC=150°,
而∠EBA=60°,所以∠ABC=90°,
在Rt△ABC中,tan60°=![]() ,
,
![]() ≈69.3(海里).
≈69.3(海里).
答:此时渔政船距钓鱼岛A的距离AB约为69.3海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离;|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数﹣5、﹣1、3,那么A到B的距离是 ,
A到C的距离是 . (直接填最后结果).
问题(2):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(3):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(4):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们排成方队做操,李明在第10列第8行,用数对表示为________,小方所在的位置用数对表示为(8,7),她在第________列第________行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)7a+3b+2b﹣5a
(2)5(﹣3x+4y)﹣6(2x﹣3y) -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=5x+m的图象过点(1,10),则该图象与x轴的交点坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)5x>3(x﹣2)+2
(2)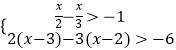 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,过点
 (
(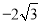 ,
,  )的直线
)的直线 交
交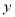 轴的正半轴于点
轴的正半轴于点 ,
,  .
.(1)求直线
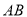 的解析式;(直接写出结果)
的解析式;(直接写出结果)(2)如图2,点
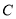 是
是 轴上一动点,以
轴上一动点,以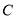 为圆心,
为圆心, 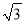 为半径作⊙
为半径作⊙ ,当⊙
,当⊙ 与
与 相切时,设切点为
相切时,设切点为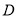 ,求圆心
,求圆心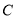 的坐标;
的坐标;(3)在(2)的条件下,点
 在
在 轴上,△
轴上,△ 是以
是以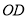 为底边的等腰三角形,求过点
为底边的等腰三角形,求过点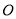 、
、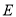 、
、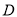 三点的抛物线.
三点的抛物线.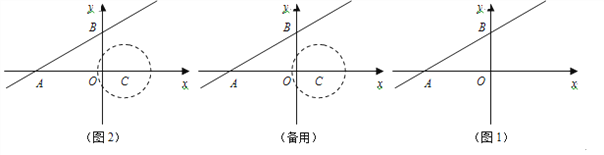
相关试题

