【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离;|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数﹣5、﹣1、3,那么A到B的距离是 ,
A到C的距离是 . (直接填最后结果).
问题(2):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(3):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(4):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
参考答案:
【答案】(1)4,8(2)|x﹣(-2)|+|x﹣1|或|x+2|+|x﹣1|(3)①-2或4②4;
【解析】试题分析: ![]()
![]() 到
到![]() 的距离是
的距离是![]()
![]() 到
到![]() 的距离是
的距离是![]()
![]() 根据题意:
根据题意: ![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和表示为:
的距离之和表示为: ![]() 或
或![]() .
.
![]() ①
①![]() 表示
表示![]() 到点
到点![]() 和点
和点![]() 距离之和等于
距离之和等于![]() .根据两点之间的距离公式,即可解出答案.②可以在不小于
.根据两点之间的距离公式,即可解出答案.②可以在不小于![]() 且不大于
且不大于![]() 的范围内任取一个数,即可算出最小值.
的范围内任取一个数,即可算出最小值.
![]() 在不小于
在不小于![]() 且不大于
且不大于![]() 的范围内值不变,最小值在这个范围内任取一个数代入即可.
的范围内值不变,最小值在这个范围内任取一个数代入即可.
![]() 要使
要使![]() |的值最小
|的值最小![]() 的值只要取
的值只要取![]() 到
到![]() 之间(包括
之间(包括![]() )的任意一个数,要使
)的任意一个数,要使![]() 的值最小,
的值最小, ![]() 应取
应取![]() ,显然当
,显然当![]() 时能同时满足要求,把
时能同时满足要求,把![]() 代入原式计算即可.
代入原式计算即可.
试题解析:
![]()
![]()
![]() |或
|或![]() .
.
![]() ①
①![]() 或
或![]()
②![]() 不小于
不小于![]() 且不大于
且不大于![]() 或
或![]()
(4)因为当不小于![]() 且不大于
且不大于![]() 时
时![]() 的最小值是
的最小值是![]()
所以当![]() 最小时
最小时![]() 有最小值.
有最小值.
所以当![]() 时,即
时,即![]() 时
时![]() 有最小值
有最小值![]()
-
科目: 来源: 题型:
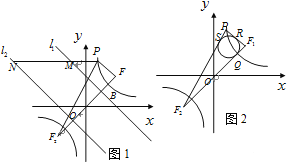
查看答案和解析>>【题目】如图1所示,已知:点
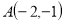 在双曲线
在双曲线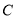 :
: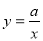 上,直线
上,直线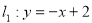 ,直线
,直线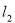 与
与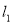 关于原点成中心对称,
关于原点成中心对称,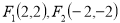 两点间的连线与曲线
两点间的连线与曲线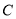 第一象限内的交点为
第一象限内的交点为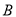 ,
,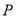 是曲线
是曲线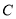 上第一象限内异于
上第一象限内异于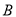 的一动点,过
的一动点,过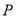 作
作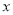 轴平行线分别交
轴平行线分别交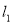 ,
,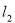 于
于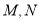 两点.
两点.(1)求双曲线
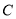 及直线
及直线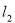 的解析式;
的解析式;(2)求证:
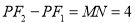 ;
;(3)如图2所示,
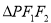 的内切圆与
的内切圆与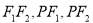 三边分别相切于点
三边分别相切于点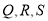 ,求证:点
,求证:点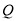 与点
与点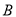 重合.(参考公式:在平面坐标系中,若有点
重合.(参考公式:在平面坐标系中,若有点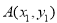 ,
,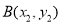 ,则A、B两点间的距离公式为=
,则A、B两点间的距离公式为=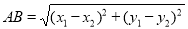 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式a2b﹣2ab+b分解因式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b不经过第三象限,则k、b应满足( )
A.k>0,b<0
B.k<0,b>0
C.k<0 b<0
D.k<0,b≥0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-b=-3,c+d=2,则2(d+c)-(a-b)的值是( )
A. 1 B. -1 C. 7 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法把17.8961精确到百分位,得到的近似值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上将点A向右移动7个单位,再向左移动4个单位,终点恰好是原点,则点A表示的数是 .
相关试题

