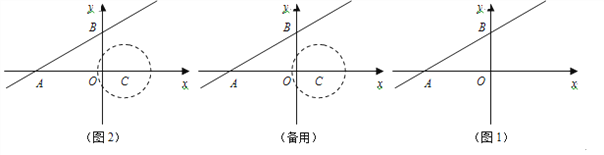
【题目】如图1,在平面直角坐标系中,过点![]() (
(![]() ,
, ![]() )的直线
)的直线![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() ,
, ![]() .
.
(1)求直线![]() 的解析式;(直接写出结果)
的解析式;(直接写出结果)
(2)如图2,点![]() 是
是![]() 轴上一动点,以
轴上一动点,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() ,当⊙
,当⊙![]() 与
与![]() 相切时,设切点为
相切时,设切点为![]() ,求圆心
,求圆心![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在
在![]() 轴上,△
轴上,△![]() 是以
是以![]() 为底边的等腰三角形,求过点
为底边的等腰三角形,求过点![]() 、
、![]() 、
、![]() 三点的抛物线.
三点的抛物线.
参考答案:
【答案】(1)直线![]() 的解析式为
的解析式为![]() ;
;
(2)当⊙![]() 与
与![]() 相切时,点
相切时,点![]() 坐标为(
坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)过点![]() 、
、![]() 、
、![]() 三点的抛物线为
三点的抛物线为![]() 或
或![]()
【解析】试题分析:(1)、根据Rt△AOB的性质求出点B的坐标,然后根据待定系数法求出函数解析式;(2)、根据⊙![]() 在直线AB的左侧和右侧两种情况以及圆的切线的性质分别求出AC的长度,从而得出点C的坐标;(3)、本题也需要分两种情况进行讨论:⊙
在直线AB的左侧和右侧两种情况以及圆的切线的性质分别求出AC的长度,从而得出点C的坐标;(3)、本题也需要分两种情况进行讨论:⊙![]() 在直线
在直线![]() 的右侧相切时得出点D的坐标,根据等边△
的右侧相切时得出点D的坐标,根据等边△![]() 的性质得出
的性质得出![]() 的坐标,从而根据待定系数法求出抛物线的解析式;⊙
的坐标,从而根据待定系数法求出抛物线的解析式;⊙![]() 在直线
在直线![]() 的左侧相切时,根据切线的直角三角形的性质求出点
的左侧相切时,根据切线的直角三角形的性质求出点![]() 的坐标,根据待定系数法求出抛物线的解析式.
的坐标,根据待定系数法求出抛物线的解析式.
试题解析:(1)∵![]() (
(![]() ,
, ![]() ),∴
),∴![]() . 在Rt△
. 在Rt△![]() 中,
中, ![]() .
.
![]() ,
, ![]() .
. ![]() . ∴
. ∴![]() (
(![]() ,
, ![]() ).
).
设直线![]() 的解析式为
的解析式为![]() .
.
则 解得
解得 ∴直线
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)如图3,①当⊙![]() 在直线
在直线![]() 的左侧时, ∵⊙
的左侧时, ∵⊙![]() 与
与![]() 相切,∴
相切,∴![]() .
.
在Rt△![]() 中,
中, ![]() .
. ![]() ,
, ![]() ,
, ![]() .
.
而![]() ,∴
,∴![]() 与
与![]() 重合,即
重合,即![]() 坐标为(
坐标为(![]() ,
, ![]() ).
).
②根据对称性,⊙![]() 还可能在直线
还可能在直线![]() 的右侧,与直线
的右侧,与直线![]() 相切,此时
相切,此时![]() .
.
∴![]() 坐标为(
坐标为(![]() ,
, ![]() ).
).
综上,当⊙![]() 与
与![]() 相切时,点
相切时,点![]() 坐标为(
坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
(3)如图4,①⊙ ![]() 在直线
在直线![]() 的右侧相切时,点
的右侧相切时,点![]() 的坐标为(
的坐标为(![]() ,
, ![]() ).
).
此时△![]() 为等边三角形.∴
为等边三角形.∴![]() (
(![]() ,
, ![]() ).
).
设过点![]() 、
、![]() 、
、![]() 三点的抛物线的解析式为
三点的抛物线的解析式为![]() .
.
则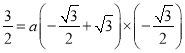
![]()
②当⊙![]() 在直线
在直线![]() 的左侧相切时,
的左侧相切时, ![]() (
(![]() ,
, ![]() )
)
设![]() ,则
,则![]() ,
, ![]() . 在Rt△
. 在Rt△![]() 中,
中, ![]() .
.
![]() , 即
, 即![]() ,
,
![]() ∴
∴![]() (
(![]() ,
, ![]() ).
).
设过点![]() 、
、![]() 、
、![]() 三点的抛物线的解析式为
三点的抛物线的解析式为![]() .
.
则![]() ,
, ![]() .
. ![]() .
.
综上,过点![]() 、
、![]() 、
、![]() 三点的抛物线为
三点的抛物线为![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中
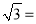 1.732)
1.732)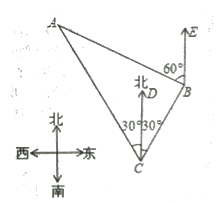
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=5x+m的图象过点(1,10),则该图象与x轴的交点坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)5x>3(x﹣2)+2
(2)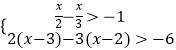 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a+5,a-3)在y轴上,则点M的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )
A.100(1+x)2=81
B.100(1﹣x)2=81
C.100(1﹣x%)2=81
D.100x2=81 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形一个角的外角是150°,则这个三角形余下两角之和是( )
A. 60° B. 90° C. 120° D. 150°
相关试题

