【题目】如图,已知直线![]() 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作![]() ,垂足为D.
,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
参考答案:
【答案】(1)证明见解析;(2)6.
【解析】分析:(1)连接OC,根据题意可证得∠CAD+∠DCA=90°,再根据角平分线的性质,得∠DCO=90°,则CD为 O的切线;
(2)过O作OF⊥AB,则∠OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形,设AD=x,在Rt△AOF中,由勾股定理得(5-x)![]() +(6-x)
+(6-x)![]() =25,从而求得x的值,由勾股定理得出AB的长.
=25,从而求得x的值,由勾股定理得出AB的长.
本题解析

(1)证明:连接OC,∵OA=OC,∴∠OCA=∠OAC,∵AC平分∠PAE,
∴∠DAC=∠CAO,∴∠DAC=∠OCA,∴PB∥OC,∵CD⊥PA,
∴CD⊥OC,CO为O半径,∴CD为O的切线;
(2)过O作OF⊥AB,垂足为F,∴∠OCD=∠CDA=∠OFD=90,∴四边形DCOF为矩形,∴OC=FD,OF=CD.∵DC+DA=6,设AD=x,则OF=CD=6x,∵O的直径为10,∴DF=OC=5,∴AF=5x,
在Rt△AOF中,由勾股定理得AF![]() +OF
+OF![]() =OA
=OA![]() .
.
即(5x) ![]() +(6x)
+(6x) ![]() =25,化简得x
=25,化简得x![]() 11x+18=0,
11x+18=0,
解得![]() .
.
∵CD=6x大于0,故x=9舍去,∴x=2,从而AD=2,AF=52=3,
∵OF⊥AB,由垂径定理知,F为AB的中点,∴AB=2AF=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=
 AB.
AB.(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学完二次根式一章后,小易同学看到这样一题:“函数
 中,自变量
中,自变量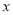 的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量
的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量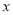 的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:第一步:函数
 中,自变量
中,自变量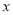 的取值范围是_____________.
的取值范围是_____________.第二步:根据自变量取值范围列表:
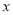
-1
0
1
2
3
4

0
1


2

 __________.
__________.第三步:描点画出函数图象.
在描点的时候,遇到了
 ,
, 这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
你能否从中得到启发,在下面的
 轴上标出表示
轴上标出表示 、
、 、
、 的点,并画出
的点,并画出 的函数图象.
的函数图象.
第四步:分析函数的性质.
请写出你发现的函数的性质(至少写两条):
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步:利用函数
 图象解含二次根式的方程和不等式.
图象解含二次根式的方程和不等式.(1)请在上面坐标系中画出
 的图象,并估算方程
的图象,并估算方程 的解.
的解.(2)不等式
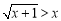 的解是__________________.
的解是__________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】小易同学在数学学习时,遇到这样一个问题:如图,已知点
 在直线
在直线 外,请用一把刻度尺(仅用于测量长度和画直线),画出过点
外,请用一把刻度尺(仅用于测量长度和画直线),画出过点 且平行于
且平行于 的直线,并简要说明你的画图依据.
的直线,并简要说明你的画图依据.
小易想到一种作法:
①在直线
 上任取两点
上任取两点 、
、 (两点不重合);
(两点不重合);②利用刻度尺连接
 并延长到
并延长到 ,使
,使 ;
;③连接
 并量出
并量出 中点
中点 ;
;④作直线
 .
.∴直线
 即为直线
即为直线 的平行线.
的平行线.
(1)请依据小易同学的作法,补全图形.
(2)证明:∵
 ,
,∴
 为
为 的中点,
的中点,又∵
 为
为 中点,
中点, ∴
 ( )
( ) (3)你还有其他画法吗?请画出图形,并简述作法.
作法:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.

(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰
 ,
, ,
, 平分
平分 ,
, 为
为 上一动点,作
上一动点,作 平行
平行 ,交
,交 于F,在
于F,在 上取一点
上取一点 ,使得
,使得 ,连接
,连接 .
.(1)根据题意补全图形;
(2)求证四边形
 是平行四边形;
是平行四边形;(3)若
 ,写出一个
,写出一个 的度数,使得四边形
的度数,使得四边形 是菱形.
是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长都是1.
 均在网格的格点上.
均在网格的格点上.(1)直接写出四边形
 的面积与
的面积与 、
、 的长度;
的长度;(2)
 是直角吗?请说出你的判断理由.
是直角吗?请说出你的判断理由.(3)找到一个格点
 ,并画出四边形
,并画出四边形 ,使得其面积与四边形
,使得其面积与四边形 的面积相等.
的面积相等.解:(1)
 ___________;
___________;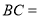 ___________;
___________;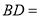 ___________.
___________.(2)判断___________(填“是”或“否”)
理由_________________________________________________;
(3)在图中画出一个满足条件的四边形
 .
.
相关试题

