Question

【题目】学完二次根式一章后，小易同学看到这样一题：“函数中,自变量的取值范围是什么？”这个问题很简单，根据二次根式的性质很容易得到自变量的取值范围.联想到一次函数，小易想进一步研究这个函数的图象和性质.以下是他的研究步骤：

第一步：函数中,自变量的取值范围是_____________.

第二步：根据自变量取值范围列表：

	-1	0	1	2	3	4
	0	1			2

__________.

第三步：描点画出函数图象.

在描点的时候，遇到了，这样的点，小易同学用所学勾股定理的知识，找到了画图方法，如图所示：

你能否从中得到启发，在下面的轴上标出表示 、、的点，并画出的函数图象.

第四步：分析函数的性质.

请写出你发现的函数的性质(至少写两条)：

____________________________________________________________________________________________

____________________________________________________________________________________________

第五步：利用函数图象解含二次根式的方程和不等式.

（1）请在上面坐标系中画出的图象，并估算方程的解.

（2）不等式的解是__________________.

Answer 1

【答案】第一步： ；第二步： ；第三步：见解析；第四步：性质一：y随x的增大而增大；性质二：函数图象只有一个点在x轴上，其余的都在x轴上方；第五步：（1）函数图象见解析， ；（2） ．

【解析】

第一步：根据二次根式有意义的条件即可求解；

第二步：将代入中即可求出m的值；

第三步：利用勾股定理即可在轴上标出表示 、、的点，然后描点并连线即可；

第四步：根据函数图象即可得出函数的性质；

第五步：（1）首先画出的图象，然后根据两函数的交点即可估算方程的解；

（2）数形结合即可得出答案．

第一步：，

∴ ，

∴自变量的取值范围是；

第二步：当时，；

第三步：根据勾股定理有

图象如图：

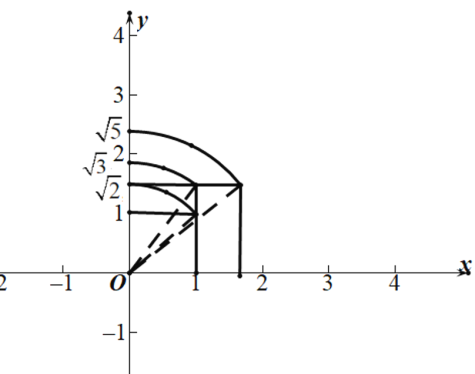
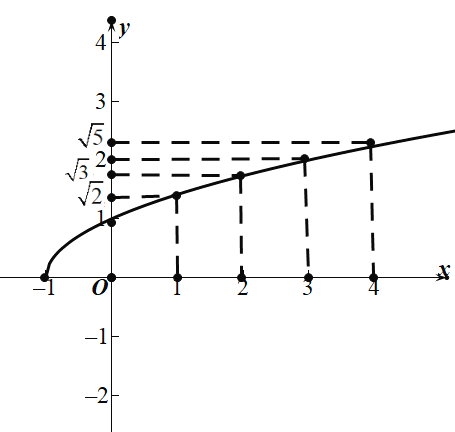
第四步：性质一：y随x的增大而增大；

性质二：函数图象只有一个点在x轴上，其余的都在x轴上方．

第五步：（1）函数图象如下，根据两函数图象的交点估算方程的解为

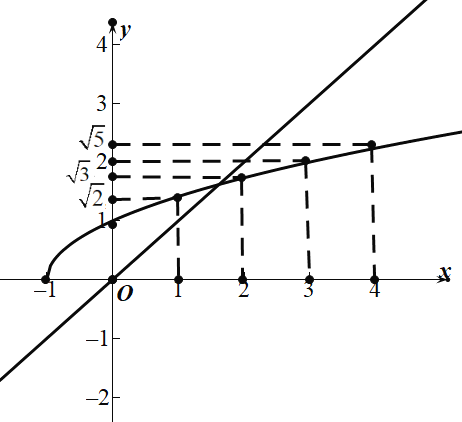
（2）根据图象可知，当时，x的取值范围为 ．