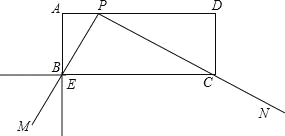
【题目】如图,在矩形ABCD中,AB=3,AD=10,将∠MPN的顶点P在矩形ABCD的边AD上滑动,在滑动过程中,始终保持∠MPN=90°,射线PN经过点C,射线PM交直线AB于点E,交直线BC于点F.
(1)求证:△AEP∽△DPC;
(2)在点P的运动过程中,点E与点B能重合吗?如果能重合,求DP的长;
(3)是否存在这样的点P使△DPC的面积等于△AEP面积的4倍?若存在,求出AP的长;若不存在,请证明理由.

参考答案:
【答案】(1)证明详见解析;(2)点E与点B能重合,B,E重合时DP的长为1或9;(3) 存在满足条件的点P,AP=1.5.
【解析】
试题分析:(1)根据矩形的性质,推出∠D=∠A=90°,再由直角三角形的性质,得出∠PCD+∠DPC=90°,又因∠CPE=90°,推出∠EPA+∠DPC=90°,∠PCD=∠EPA,从而证明△CDP∽△PAE;
(2)利用当B,E重合时,利用已知得出△ABP∽DPC,进而求出DP的长即可;
(3)假设存在满足条件的点P,设DP=x,则AP=10﹣x,由△CDP∽△PAE知,求出DP即可.
试题解析:(1)∵四边形ABCD是矩形,
∴∠D=∠A=90°,CD=AB=6,
∴∠PCD+∠DPC=90°,
又∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴△AEP∽△DPC;
(2)假设在点P的运动过程中,点E能与点B重合,
当B,E重合时,
∵∠BPC=90°,
∴∠APB+∠DPC=90°,
∵∠DPC+∠DCP=90°,
∴∠DCP=∠APB,
∵∠A=∠D,
∴△ABP∽DPC,
∴![]() ,
,
即![]() ,
,
解得:DP=1或9,
∴B,E重合时DP的长为1或9;
(3)存在满足条件的点P,
∵△CDP∽△PAE,
根据使△DPC的面积等于△AEP面积的4倍,得到两三角形的相似比为2,
∴![]() =2,
=2,
即![]() =2,
=2,
解得AP=1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2+ab=15,b2+ab=6,则a2-b2=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(
 =1.7).
=1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代入消元法解下列方程
(1)
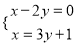 (2)
(2) 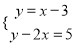
(3)
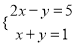 (4)
(4)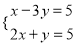
(5)
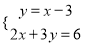 (6)
(6)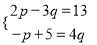
-
科目: 来源: 题型:
查看答案和解析>>【题目】用加减消元法解下列方程
(1)
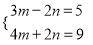 (2)
(2)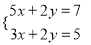
(3)
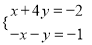 (4)
(4)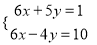
(5)
 (6)
(6) 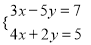
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:
 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|+(b﹣1)2=0,那么代数式(a+b)2017的值是( )
A.2009
B.﹣2009
C.1
D.﹣1
相关试题

