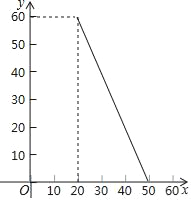
【题目】某商店经销一种小家电,每个小家电的成本为20元,市场调查发现,该种小家电每天的销售量y(个)与销售单价x(元)的函数图象如图.设这种小家电每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)如果物价部门规定这种小家电的销售单价不高于32元,该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为多少元?
参考答案:
【答案】(1)w=﹣2x2+140x﹣2000;(2)该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为30元.
【解析】试题分析:(1)先求得销售量y(个)与销售单价x(元)的函数关系式,再根据“利润=销售量×(销售单价-成本)”即可得;
(2)将w=400代入(1)中的关系式,解方程后进行比较即可得.
试题解析:(1)设y=kx+b,
则![]() ,
,
解得: ![]() ,
,
则y=﹣2x+100(20≤x≤50),
所以w=(x﹣20)(﹣2x+100)=﹣2x2+140x﹣2000;
(2)根据题意,得:﹣2x2+140x﹣2000=400,
解得:x=30或x=40,
因为x≤32,
所以x=30,
答:该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为30元.
-
科目: 来源: 题型:
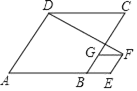
查看答案和解析>>【题目】如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+
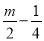 =0的两个实数根.
=0的两个实数根.(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,A是y=﹣
 (x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
(x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ADE≌△CBF;
(2)连结CE,AF,求证:四边形AFCE为平行四边形.

-
科目: 来源: 题型:
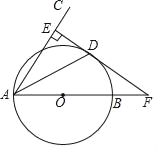
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,过点D作DE⊥AC于E.
(1)求证:ED是⊙O的切线;
(2)若ED,AB的延长线相交于F,且AE=5,EF=12,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm,动点N从点C出发,沿线段CB以2cm/s的速度向点B运动,并在达到点B后,立即以同样的速度返回向点C运动;同时动点M从点B出发,沿折线B﹣A﹣C以1cm/s的速度向点C运动,当点N回到点C时,两个动点同时停止运动.⊙M是以M为圆心,1cm为半径的圆,设运动时间为t(s) (t>0)
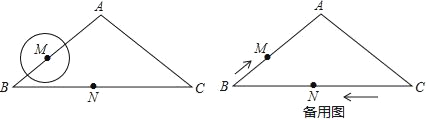
(1)tanB= ;
(2)当点M在线段AB上运动,且⊙M与BC相切时,求t的值;
(3)当t为何值时,⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧,且经过交点和点N的直线与⊙M相切?
相关试题

