【题目】如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为_____.
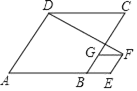
参考答案:
【答案】![]()
【解析】
延长FG交AD于点M,过点D作DH⊥AB交AB于点H,交GF的延长线于点N,由菱形的性质和勾股定理再结合已知条件可求出NF,DN的长,在直角三角形DNF中,再利用勾股定理即可求出DF的长.
延长FG交AD于点M,过点D作DH⊥AB交AB于点H,交GF的延长线于点N,
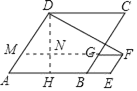
∵四边形ABCD和四边形BEFG都是菱形,
∴GF∥BE,EF∥AM,
∴四边形AMFE是平行四边形,
∴AM=EF=2,MF=AE=AB+BE=5+2=7,
∴DM=AD﹣AM=5﹣2=3,
∵∠A=60°,
∴∠DAH=30°,
∴MN=![]() DM=
DM=![]() ,
,
∴DN=![]() =
=![]() ,NF=MF﹣MN=
,NF=MF﹣MN=![]() ,
,
在Rt△DNF中,DF=![]() =
=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两盒中各有3张卡片,卡片上分别标有数字﹣7、﹣1、3和﹣2、1、6,这些卡片除数字外都相同.把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把抽得卡片上的数字分别作为平面直角坐标系中一个点的横坐标、纵坐标.
(1)列出这样的点所有可能的坐标;
(2)求这些点落在第二象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是一位同学所做的有理数运算解题过程的一部分:
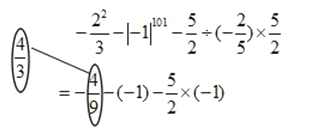
(1)请你在上面的解题过程中仿照给出的方式,圈画出他的错误之处,并将正确结果写在相应的圈内;
(2)请就此题反映出的该同学有理数运算掌握的情况进行具体评价,并对相应的有效避错方法给出你的建议。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式
 是关于
是关于 的二次多项式.
的二次多项式.(1)若关于
 的方程
的方程 的解是
的解是 ,求
,求 的值;
的值;(2)若当
 时,代数式
时,代数式 的值为-39,求当
的值为-39,求当 时,代数式
时,代数式 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+
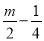 =0的两个实数根.
=0的两个实数根.(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,A是y=﹣
 (x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
(x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____. -
科目: 来源: 题型:
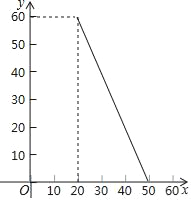
查看答案和解析>>【题目】某商店经销一种小家电,每个小家电的成本为20元,市场调查发现,该种小家电每天的销售量y(个)与销售单价x(元)的函数图象如图.设这种小家电每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)如果物价部门规定这种小家电的销售单价不高于32元,该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为多少元?
相关试题

