【题目】平面直角坐标系中,A是y=﹣![]() (x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
(x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
参考答案:
【答案】(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
【解析】
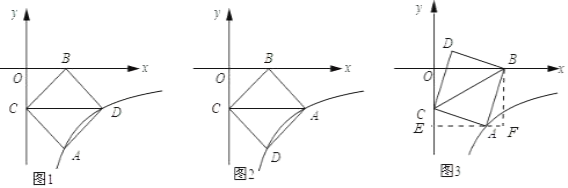
首先依据题意画图图形,对于图1和图2依据正方形的对称性可得到点D的坐标,对于图3可证明△AEC≌△BFA,从而可得到AE=BF,然后由反比例函数的解析式可求得点A的坐标,然后可得到点D的坐标.
如图1所示:当CD为对角线时.
∵OC=2,AB=CD=4,
∴D(4,﹣2).
如图2所示:
∵OC=2,BD=AC=4,
∴D(2,﹣4).
如图3所示:过点A作AE⊥y轴,BF⊥AE,则△AEC≌△BFA.
∴AE=BF.
设点A的横纵坐标互为相反数,
∴A(2![]() ,﹣2
,﹣2![]() )
)
∴D(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
综上所述,点D的坐标为(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
故答案为:(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式
 是关于
是关于 的二次多项式.
的二次多项式.(1)若关于
 的方程
的方程 的解是
的解是 ,求
,求 的值;
的值;(2)若当
 时,代数式
时,代数式 的值为-39,求当
的值为-39,求当 时,代数式
时,代数式 的值.
的值. -
科目: 来源: 题型:
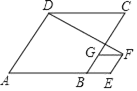
查看答案和解析>>【题目】如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+
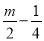 =0的两个实数根.
=0的两个实数根.(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
-
科目: 来源: 题型:
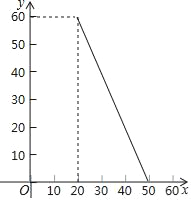
查看答案和解析>>【题目】某商店经销一种小家电,每个小家电的成本为20元,市场调查发现,该种小家电每天的销售量y(个)与销售单价x(元)的函数图象如图.设这种小家电每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)如果物价部门规定这种小家电的销售单价不高于32元,该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ADE≌△CBF;
(2)连结CE,AF,求证:四边形AFCE为平行四边形.

-
科目: 来源: 题型:
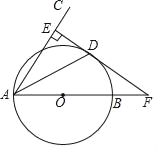
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,过点D作DE⊥AC于E.
(1)求证:ED是⊙O的切线;
(2)若ED,AB的延长线相交于F,且AE=5,EF=12,求BF的长.
相关试题

