【题目】如图,线段AB和CD数轴上运动,A开始时与原点重合,且![]() .
.
(1)若AB=10,且B为线段AC的中点,求线段AD的长.
(2)在(1)的条件下,线段AB和CD同时开始向右运动,线段AB的速度为5个单位/秒,线段CD的速度为3个单位/秒,经过t秒恰好有![]() ,求t的值.
,求t的值.
(3)若线段AB和CD同时开始向左运动,且线段AB的速度大于线段CD的速度,在点A和C之间有一点P(不与点B重合),且有![]() ,此时线段BP为定值吗?若是请求出这个定值,若不是请说明理由.
,此时线段BP为定值吗?若是请求出这个定值,若不是请说明理由.
![]()
参考答案:
【答案】(1)52;(2)t=6或25;(3)BP=1为定值,理由见解析.
【解析】
(1)根据![]() ,AB=10,求出CD长,再由B为线段AC的中点,求出AC长,即可求出AD;
,AB=10,求出CD长,再由B为线段AC的中点,求出AC长,即可求出AD;
(2)由题知A:5t,B:10+5t,C:20+3t,D:52+3t,再写出AC和BD长,代入![]() 中解出t即可;
中解出t即可;
(3)由![]() ,在点A和C之间有一点P,得到
,在点A和C之间有一点P,得到![]() ,
,![]() ,化简即可证明BP为定值.
,化简即可证明BP为定值.
解:(1)∵![]() ,AB=10,
,AB=10,
∴![]() ,
,
∵B为线段AC的中点,
∴![]() ,
,
∴![]() ;
;
(2)由题知A:5t,B:10+5t,C:20+3t,D:52+3t,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
①当0≤t<10时,![]() ,解得:
,解得:![]() ,0≤6<10,成立;
,0≤6<10,成立;
②当10≤t<21时,![]() ,方程无解;
,方程无解;
③当21≤t时,![]() ,解得:
,解得:![]() ,21≤25,成立;
,21≤25,成立;
t=6或25;
(3)∵![]() ,在点A和C之间有一点P ,
,在点A和C之间有一点P ,
∴![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
∴BP=1,为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某购物网站上一种小礼品按销售量分三部分制定阶梯销售单价,如下表:
销售量
单价
不超过120件的部分
3.5元/件
超过120件不超过300件的部分
3.2元/件
超过300件的部分
3.0元/件
(1)“双十一”期间,购物总金额累计满300元可使用50元购物津贴(即累计总金额每满300减50元),若购买85件,花费 元;若购买120件,花费 元;若购买250件,花费 元.
(2)“双十一”期间,王老师购买这种小礼品花了335元,列方程求王老师购买了这种小礼品多少件?
(3)“双十二”即将来临,但“双十二”期间不能使用购物津贴,王老师和李老师各自单独购买这种小礼品共400件,其中王老师的购买数量大于李老师的购买数量,她们一共花费1336元,请问王老师和李老师各购买这种小礼品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上
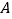 点、
点、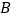 点表示的数分别为
点表示的数分别为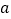 、
、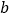 ,则
,则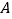 、
、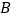 两点之间的距离
两点之间的距离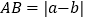 ,线段
,线段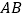 的中点
的中点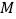 表示的数为
表示的数为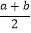 .
.(问题情境)
在数轴上,点
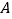 表示的数为-20,点
表示的数为-20,点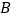 表示的数为10,动点
表示的数为10,动点 从点
从点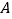 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点 也从点
也从点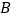 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时, 、
、 两点相遇,且动点
两点相遇,且动点 、
、 运动的速度之比是
运动的速度之比是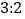 (速度单位:单位长度/秒).
(速度单位:单位长度/秒).

备用图
(综合运用)
(1)点
 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;(2)当
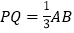 时,求运动时间;
时,求运动时间;(3)若点
 、
、 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点 、
、 的运动,线段
的运动,线段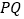 的中点
的中点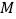 也随着运动.问点
也随着运动.问点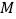 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从 、
、 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点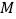 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔
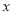 (
(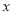 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)(2)当购买钢笔多少支时,在两店购买付款一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )

A. (0,0); B. (0,1); C. (0,2); D. (0,3).
相关试题

