搜索
【题目】如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（ ）
A. （0，0）； B. （0，1）； C. （0，2）； D. （0，3）．
参考答案：
【答案】D
【解析】试题分析：根据轴对称作最短路线得出AE=B′E，进而得出B′O=C′O，即可得出△ABC的周长最小时C点坐标．
解：作B点关于y轴对称点B′点，连接AB′，交y轴于点C′，
此时△ABC的周长最小，
∵点A、B的坐标分别为（1，4）和（3，0），
∴B′点坐标为：（﹣3，0），AE=4，
则B′E=4，即B′E=AE，
∵C′O∥AE，
∴B′O=C′O=3，
∴点C′的坐标是（0，3），此时△ABC的周长最小．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AB和CD数轴上运动，A开始时与原点重合，且
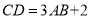.(1)若AB=10，且B为线段AC的中点，求线段AD的长.
(2)在(1)的条件下，线段AB和CD同时开始向右运动，线段AB的速度为5个单位/秒，线段CD的速度为3个单位/秒，经过t秒恰好有
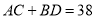，求t的值.(3)若线段AB和CD同时开始向左运动，且线段AB的速度大于线段CD的速度，在点A和C之间有一点P(不与点B重合)，且有
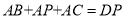，此时线段BP为定值吗？若是请求出这个定值，若不是请说明理由.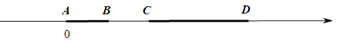
-
科目： 来源： 题型：
查看答案和解析>>【题目】（背景知识）
数轴是初中数学的一个重要工具，利用数轴可以将数与形完美结合．研究数轴我们发现有许多重要的规律:
例如，若数轴上
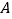点、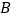
点表示的数分别为
、
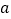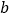，则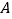、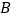两点之间的距离
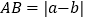，线段
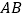的中点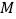
表示的数为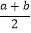
．（问题情境）
在数轴上，点
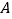表示的数为-20，点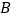表示的数为10，动点
从点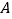出发沿数轴正方向运动，同时，动点
也从点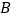出发沿数轴负方向运动，已知运动到4秒钟时，、两点相遇，且动点、运动的速度之比是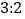
（速度单位:单位长度/秒）．
备用图
（综合运用）
（1）点
的运动速度为______单位长度/秒，点的运动速度为______单位长度/秒；（2）当
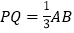时，求运动时间；（3）若点
、在相遇后继续以原来的速度在数轴上运动，但运动的方向不限，我们发现:随着动点、的运动，线段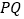
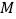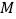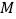的中点也随着运动．问点能否与原点重合？若能，求出从、相遇起经过的运动时间，并直接写出点的运动方向和运动速度；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学七年级开展演讲比赛，学校决定购买一些笔记本和钢笔作为奖品．现了解情况如下：甲、乙两家商店出售两种同样品牌的笔记本和钢笔．笔记本定价为每本20元，钢笔每支定价5元，经洽谈后，甲店每买一本笔记本赠一支钢笔；乙店全部按定价的9折优惠．七年级需笔记本20本，钢笔若干支（不小于20支）．问：
（1）如果购买钢笔
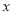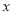（不小于20）支，则在甲店购买需付款 ______ 元，在乙店购买需付款 _______________ 元．（用x的代数式表示）（2）当购买钢笔多少支时，在两店购买付款一样？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标；
(3)在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶．甲出发2h后到达B地立即按原路返回，返回时速度提高了30km/h，回到A地后在A地休息等乙，乙在出发5h后到达A地．(友情提醒：可以借助用线段图分析题目）
（1）乙的速度是_______
，甲从A地到B地的速度是_______，甲在出发_______小时到达A地．（2）出发多长时间两人首次相遇？
（3）出发多长时间时，两人相距30千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
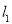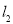分别表示使用一种白炽灯和一种节能灯的费用
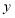（费用
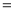灯的售价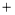
电费，单位：元）与照明时间
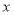（小时）的函数图象，假设两种灯的使用寿命都是
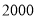小时，照明效果一样.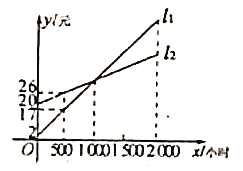
（1）根据图象分别求出
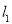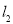，的函数表达式；（2）小亮认为节能灯一定比白炽灯省钱，你是如何想的？
相关试题
