【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

参考答案:
【答案】(1)详见解析;(2)四边形EBFD为菱形.
【解析】
(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;
(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
∵AE=CF,
∴AO-AE=CO-CF,
即EO=FO.
在△BOE和△DOF中,
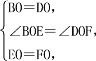
∴△BOE≌△DOF(SAS).
(2)四边形EBFD为菱形,
证明:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形.
∵BD⊥EF,
∴四边形EBFD为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分)
70
80
90
男生(人)
5
10
7
女生(人)
4
13
4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图所示,已知点C在线段AB上,线段AB=12,点M,N分别是AC,BC的中点,求线段MN的长度.
(2)把(1)中的“点C在线段AB上”改为“点C在线段AB延长上”,其他条件均不变,画图并求出线段MN的长度;
(3)已知线段AB,点C为直线AB外任意一点,点M,N分别是AC,BC的中点,连接MN,画图并猜想线段MN与线段AB的数量关系.(只要求画图,写出结论)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )

A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
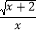 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=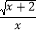 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:(1)函数y=
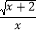 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下表是y与x的几组对应值.
x
-2
-

-1
-



1
2
3
4
…
y
0
-

-1
-

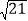


m


…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
-
科目: 来源: 题型:
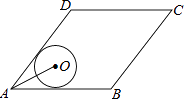
查看答案和解析>>【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
A.5
B.6
C.2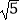
D.3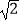
相关试题

