【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.
(I)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.

参考答案:
【答案】(1)∠BAD=22°;(2)56°或18°.
【解析】试题分析:(1)由BE为∠ABC的平分线,得出∠BAD=22°,再求出∠C,得出∠CAD=52°,即可得出结论;(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
解:(1)∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°﹣34°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°。
(2)当∠EFC=90°时,∠BEF=90°﹣∠CBE=56°,
当∠FEC=90°时,∠BEF=180°-72°﹣90°=18°,
故答案为:56°或18°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数9的平方根是()
A. -3 B. 3 C. ±3 D. 81
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形的边长是 2cm,设它的边长增加 x cm时,正方形的面积增加 y cm2,求y与x之间的函数关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一副三角板可以画出的最大锐角的度数是( )
A. 85° B. 75° C. 60° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明根据的是等式的哪一条性质以及是怎样变形的.
(1)如果
 ,那么x=__________,根据____________________;
,那么x=__________,根据____________________;(2)如果-2x=2y,那么x=_________,根据____________________;
(3)如果x=3x+2,那么x-_______=2,根据____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4x=9+x;
(2)4-
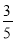 m=7;
m=7;(3)8y-3=5y+3;
(4)4x+5=3x+3-2x.
相关试题

