【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

参考答案:
【答案】(1)、证明过程见解析;(2)、AF=2![]()
【解析】试题分析:(1)、根据平行四边形的性质得出∠ADF=∠CED,∠B+∠C=180°,结合∠AFE+∠AFD=180°,∠AFE=∠B,得出∠AFD=∠C,从而得出三角形相似;(2)、根据勾股定理得出DE的长度,然后根据△ADF和△DEC相似得出答案.
试题解析:(1)、∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD, ∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,∴∠AFD=∠C, ∴△ADF∽△DEC;
(2)、∵CD=AB=4,AE⊥BC,∴AE⊥AD; 在Rt△ADE中,DE=![]() ,
,
∵△ADF∽△DEC,∴![]() ; ∴
; ∴![]() ,解得AF=.
,解得AF=.
-
科目: 来源: 题型:
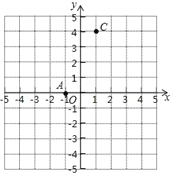
查看答案和解析>>【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数9的平方根是()
A. -3 B. 3 C. ±3 D. 81
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形的边长是 2cm,设它的边长增加 x cm时,正方形的面积增加 y cm2,求y与x之间的函数关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.
(I)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一副三角板可以画出的最大锐角的度数是( )
A. 85° B. 75° C. 60° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明根据的是等式的哪一条性质以及是怎样变形的.
(1)如果
 ,那么x=__________,根据____________________;
,那么x=__________,根据____________________;(2)如果-2x=2y,那么x=_________,根据____________________;
(3)如果x=3x+2,那么x-_______=2,根据____________________.
相关试题

