【题目】定义:如果M个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M个数的祖冲之数组.如(3,6)为两个数的祖冲之数组,因为3×6能被(3+6整除);又如(15,30,60)为三个数的祖冲之数组,因为(15×30)能被(15+30)整除,(15×60)能被(15+60)整除,(30×60)能被(30+60)整除…
(1)我们发现,3和6,4和12,5和20,6和30…,都是两个数的祖冲之数组;由此猜测n和n(n﹣1)(n≥2,n为整数)组成的数组是两个数的祖冲之数组,请证明这一猜想.
(2)若(4a,5a,6a)是三个数的祖冲之数组,求满足条件的所有三位正整数a.
参考答案:
【答案】
(1)解:∵nn(n﹣1)÷[n+n(n﹣1)]=n2(n﹣1)÷n2=n﹣1,
∴n和n(n﹣1)(n≥2,n为整数)组成的数组是祖冲之数组.
(2)解:∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() 都是整数,
都是整数,
∴a是5,9,11的倍数,
∴满足条件的所有三位正整数a为495或990.
【解析】(1)根据祖冲之数组的定义,即可解决问题.(2)首先判断出a是5,9,11的倍数,由此即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同
(1)求这个相同的解;
(2)求a的值;
(3)若[m]表示不大于m的最大整数,求[
 -2]的值
-2]的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】祁阳县某中学校团委开展“关爱残疾学生”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
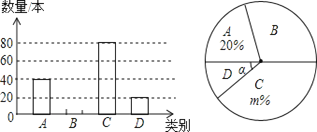
(1)这次统计共抽取了 书籍,扇形统计图中的m= ,∠α的度数是
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)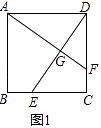
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;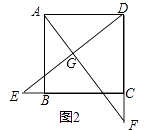
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.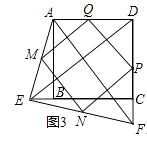
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
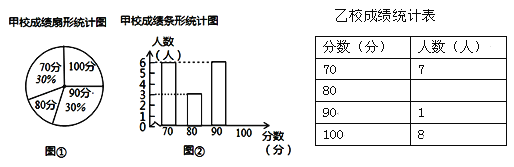
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l上有AB两点,AB=18cm,点O是线段AB上的一点,OA=2OB

(1)OA= cm , OB= cm;
(2)若点C是直线AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=3;
②当点P经过点O时,动点M从点O出发,以4cm/s的速度也向右运动.当点M追上点Q后立即返回,以4cm/s的速度向点P运动,遇到点P后再立即返回,以4cm/s的速度向点Q运动,如此往返.当点P与点Q重合时,P,Q两点停止运动.此时点M也停止运动.在此过程中,点M行驶的总路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果3y9﹣2m+2=0是关于y的一元一次方程,则m= .
相关试题

