搜索
【题目】祁阳县某中学校团委开展“关爱残疾学生”爱心捐书活动，全校师生踊跃捐赠各类书籍共3000本．为了解各类书籍的分布情况，从中随机抽取了部分书籍分四类进行统计：A．艺术类；B．文学类；C．科普类；D．其他，并将统计结果绘制成如图所示的两幅不完整的统计图．
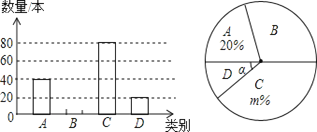
(1)这次统计共抽取了 书籍，扇形统计图中的m= ，∠α的度数是
(2)请将条形统计图补充完整；
(3)估计全校师生共捐赠了多少本文学类书籍．
参考答案：
【答案】（1）200,40,36°；（2）参见解析；（3）900本．
【解析】试题分析：（1）用A的本数÷A所占的百分比，即可得到抽取的本数；用C的本数÷总本数，即可求得m；计算出D的百分比乘以360°，即可得到圆心角的度数；（2）计算出B的本数，即可补全条形统计图；（3）根据文学类书籍的百分比，用3000乘以这个百分比即可解答．
试题解析：（1）已知部分求整体，用A的本数÷A所占的百分比，40÷20%=200（本）即为共抽取的书籍数；用C的本数÷总本数，即可求得m，80÷200=40%；计算出D的百分比乘以360°,即可得到∠α的度数: 
×360°=36°，∴依次填：200，40，36°；（2）B的本数为：200﹣40﹣80﹣20=60（本），即可补全条形统计图；（3）根据文学类书籍的百分比，用3000乘以这个百分比：3000×
=900（本）．∴估计全校师生共捐赠了900本文学类书籍．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
的对称轴为
轴，且经过(0，0)，(
)两点，点P在抛物线上运动，以P为圆心的⊙P经过定点A(0，2)，(1)求
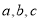的值； (2)求证：点P在运动过程中，⊙P始终与
轴相交；(3)设⊙P与
轴相交于M
，N 
(
＜
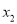)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．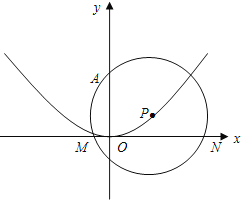
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB=115°，∠EOF =155°，OA平分∠EOC，OB平分∠DOF，
（1）求∠AOE+∠FOB度数；
（2）求∠COD度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知方程6x－9＝10x－45与方程3a－1＝3（x＋a）－2a的解相同
（1）求这个相同的解；
（2）求a的值；
（3）若[m]表示不大于m的最大整数，求[
－2]的值 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．
试探究下列问题：
（1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）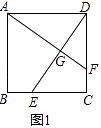
（2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；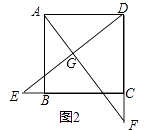
（3）如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．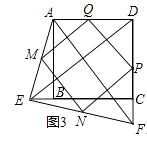
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如果M个不同的正整数，对其中的任意两个数，这两个数的积能被这两个数的和整除，则称这组数为M个数的祖冲之数组．如（3，6）为两个数的祖冲之数组，因为3×6能被（3+6整除）；又如（15，30，60）为三个数的祖冲之数组，因为（15×30）能被（15+30）整除，（15×60）能被（15+60）整除，（30×60）能被（30+60）整除…
（1）我们发现，3和6，4和12，5和20，6和30…，都是两个数的祖冲之数组；由此猜测n和n（n﹣1）（n≥2，n为整数）组成的数组是两个数的祖冲之数组，请证明这一猜想．
（2）若（4a，5a，6a）是三个数的祖冲之数组，求满足条件的所有三位正整数a． -
科目： 来源： 题型：
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并根据统计数据绘制了如下不完整的统计图表：
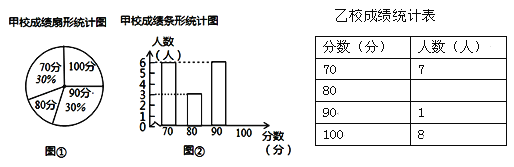
（1）在图①中，“80分”所在扇形的圆心角度数为 ；
（2）请你将图②补充完整；
（3）求乙校成绩的平均分；
（4）经计算知S甲2=135，S乙2=175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．
相关试题
