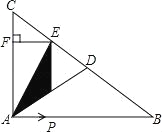
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.
(1)PE的长为 (用含t的代数式表示);
(2)求S与t之间的函数表达式;
(3)求S的最大值及S取得最大值时t的值;
(4)当S为△ABC面积的![]() 时,t的值有 个.
时,t的值有 个.
参考答案:
【答案】(1) ![]() (4-t).(2) S=
(4-t).(2) S=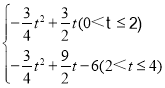 .(3)
.(3) ![]() .(4)4.
.(4)4.
【解析】
试题分析:(1)根据EP∥AC,得![]() ,列出比例式即可解决.
,列出比例式即可解决.
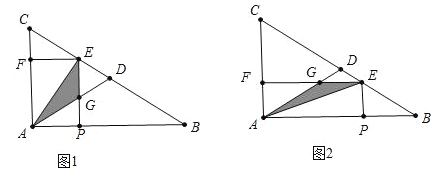
(2)分两种情形讨论①如图1中,当0<t≤2时,根据S=![]() EGAP即可计算,②如图2中,当2<t≤4时,根据S=
EGAP即可计算,②如图2中,当2<t≤4时,根据S=![]() GEAF即可计算.
GEAF即可计算.
(3)分两种情形,利用配方法根据二次函数性质即可解决.
(4)分两种情形,列出方程即可解决,注意检验是否符合题意.
试题解析:(1)如图1中,∵EP∥AC,
∴![]() ,
,
∴![]() ,
,
∴PE=![]() (4-t).
(4-t).
(2)①当0<t≤2时,
∵∠BAC=90°,CD=DB,
∴∠DAB=∠B,∵∠APG=∠BAC=90°,
∴△APG∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴PG=![]() t,
t,
∴EG=3-![]() t,
t,
∴S=![]() EGAP=-
EGAP=-![]() t2+
t2+![]() t.
t.
②当2<t≤4时如图2中,∵∠FAG=∠C,∠AFG=∠BAC,
∴△AFG∽△CAB,
∴![]() ,
,
∴FG=4-t,GE=2t-4,
∴S=![]() GEAF=-
GEAF=-![]() t2+
t2+![]() -6.
-6.
综上所述S=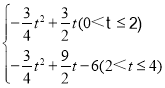 .
.
(3)当0<t≤2时,S=-![]() (t-1)2+
(t-1)2+![]() ,
,
∵-![]() <0,
<0,
∴t=1时,S最大值为![]() ,
,
当2<t≤4时,S=-![]() (t-3)2+
(t-3)2+![]() ,
,
∵-![]() <0,
<0,
∴t=3时,S最大值为![]() .
.
综上所述t=1或3时,S最大值都是![]() .
.
(4)由题意-![]() t2+
t2+![]() t=
t=![]() ,整理得到5t2-10t+4=0,t=
,整理得到5t2-10t+4=0,t=![]() 符合题意.
符合题意.
或-![]() t2+
t2+![]() t-6=
t-6=![]() ,整理得到5t2-30t+44=0,t=
,整理得到5t2-30t+44=0,t=![]() 符合题意,
符合题意,
∴S为△ABC面积的![]() 时,t的值有四个.
时,t的值有四个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算:①x2+x4=x6 ②2x+3y=5xy ③x6÷x3=x3 ④(x3)2=x6,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=
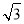 ,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.
,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.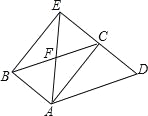
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A、0.720精确到百分位 B、5.078×104精确到千分位
C、36万精确到个位 D、2.90×105精确到千位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2016个点的坐标为( )
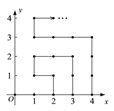
A(45,9) B(45,13) C(45,22) D(45,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
(1)求此抛物线所对应的函数表达式.
(2)求PF的长度,用含m的代数式表示.
(3)当四边形PEDF为平行四边形时,求m的值.
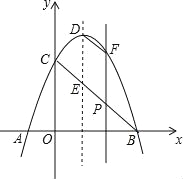
相关试题

