【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
参考答案:
【答案】(1)购进甲种花卉每盆15元,购进乙种花卉每盆12元;(2)至少购进甲种花卉81盆.
【解析】
(1)根据题意可以列出相应的二元一次方程组,从而可以求得购进甲、乙两种花卉,每盆各需多少元;
(2)设购进甲种花卉a盆,则购进乙种花卉(100-a)盆,根据“获利超过480元”列出不等式并解答.
解:(1)设购进甲种花卉每盆![]() 元,购进乙种花卉每盆
元,购进乙种花卉每盆![]() 元.
元.
![]() ,解得
,解得![]() .
.
答:购进甲种花卉每盆15元,购进乙种花卉每盆12元.
(2)设购进甲种花卉![]() 盆,则购进乙种花卉
盆,则购进乙种花卉![]() 盆.
盆.
![]() ,解得
,解得![]() .
.
∵![]() 为整数,∴
为整数,∴![]() 的最小整数值为81.
的最小整数值为81.
∴至少购进甲种花卉81盆.
-
科目: 来源: 题型:
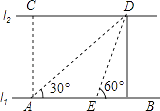
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿
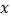 轴向右平移,当点C落在直线
轴向右平移,当点C落在直线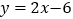 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )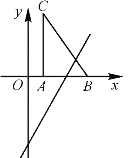
A. 16B. 8C. 8
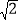 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)当
 时,直接写出
时,直接写出 的取值范围
的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知, 四边形
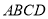 , 连接
, 连接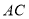 ,
,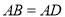 ,
,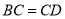 .
.(1)如图
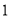 , 求证:
, 求证: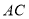 平分
平分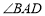 ;
;(2)如图
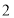 ,点
,点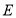 在
在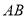 的延长线上,连接
的延长线上,连接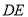 交
交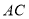 于点
于点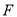 ,求证:
,求证: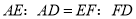 ;
;(3)如图3,在
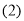 的条件下,连接
的条件下,连接 ,点
,点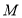 在
在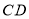 延长线上,连接
延长线上,连接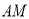 ,延长
,延长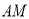 与
与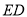 延长线交于点
延长线交于点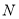 , 若
, 若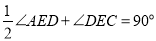 ,
,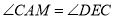 ,
, 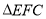 的面积与
的面积与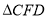 的面积比为
的面积比为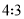 ,
, 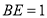 ,
,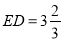 ,求
,求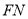 的长.
的长.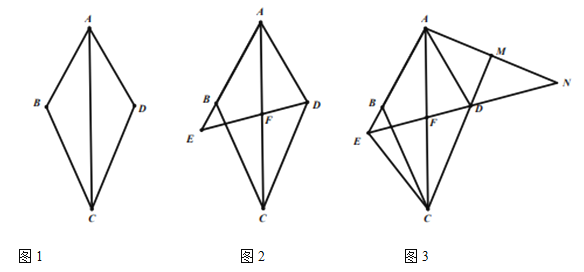
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
, ,且
,且 满足方程组
满足方程组 ,连接
,连接 ,
, .
.(1)求
 的面积;
的面积;(2)动点
 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿
个单位长度的速度沿 轴向左运动,连接
轴向左运动,连接 ,设点
,设点 运动的时间为
运动的时间为 秒,
秒,  的面积为
的面积为 , 试用含
, 试用含 的式子表示
的式子表示 ;
;(3)在
 的条件下,点
的条件下,点 ,点
,点 是
是 上一点,连接
上一点,连接 ,点
,点 在
在 延长线上,且
延长线上,且 ,连接
,连接 , 当点
, 当点 在
在 轴负半轴上,
轴负半轴上, ,
, , 四边形
, 四边形 的面积与
的面积与 的面积比为
的面积比为 时,求此时
时,求此时 值和点
值和点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;
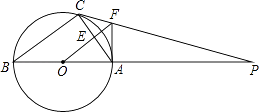
(1)判断AF与⊙O的位置关系并说明理由.
(2)若⊙O的半径为4,AF=3,求AC的长.
相关试题

