【题目】市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
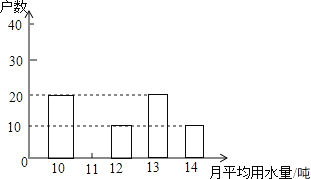
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数.
参考答案:
【答案】(1)见解析;(2)平均数是11.6吨;众数是11吨,中位数是11吨.
【解析】
试题分析:(1)利用总数100减去其它组的人数即可求得月用水量是11吨的人数,即可补全直方图;
(2)利用加权平均数公式即可求得平均数,然后根据众数和中位数的定义确定众数和中位数.
解:(1)月用水量是11吨的户数是:100﹣20﹣10﹣20﹣10=40(户);
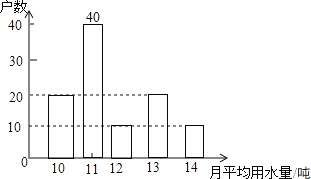 ;
;
(2)平均数是:![]() (20×10+40×11+10×12+20×13+10×14)=11.6(吨);
(20×10+40×11+10×12+20×13+10×14)=11.6(吨);
众数是11吨,中位数是11吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究:如图1,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
(2)应用:如图2,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=60°,求∠DEF的度数.
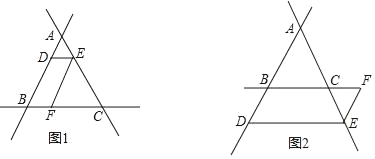
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形
 的两个顶点,以
的两个顶点,以 对角线为边作正方形
对角线为边作正方形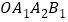 ,再以正方形的对角线
,再以正方形的对角线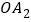 作正方形
作正方形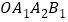 ,…,依此规律,则点
,…,依此规律,则点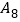 的坐标是( )
的坐标是( )
A. (-8,0) B. (0,8)
C. (0,8
 ) D. (0,16)
) D. (0,16) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.

(1)求该抛物线的函数解析式;
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
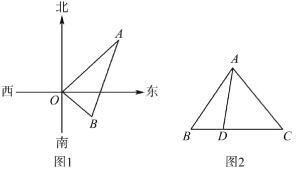
查看答案和解析>>【题目】(1)如图1,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,求水管AB的长;
(2)如图2,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是菱形ABCD的边AB,AD的中点,且AB=5,AC=6.

(1)求对角线BD的长;
(2)求证:四边形AEOF为菱形.
相关试题

