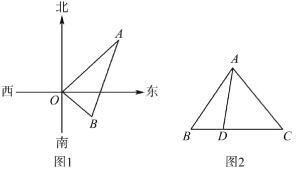
【题目】(1)如图1,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,求水管AB的长;
(2)如图2,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
参考答案:
【答案】(1)AB的长为40m;(2)CD=9.
【解析】(1)东北方向和东南方向间刚好是一直角,利用勾股定理解图中直角三角形即可;
(2)先根据勾股定理的逆定理判断出△ABD的形状,再根据勾股定理求出CD的长即可.
(1)由题意可得∠AOB=90°,
在Rt△AOB中,
AB=![]() =
=![]() =40(m),
=40(m),
答:水管AB的长为40m;
(2)∵AB=13,AD=12,BD=5,
∴![]()
∴![]() ,
,
∴∠ADB=∠ADC=90°,
在Rt△ADC中,∵AC=15,
∴CD=![]() =9.
=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形
 的两个顶点,以
的两个顶点,以 对角线为边作正方形
对角线为边作正方形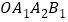 ,再以正方形的对角线
,再以正方形的对角线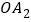 作正方形
作正方形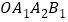 ,…,依此规律,则点
,…,依此规律,则点 的坐标是( )
的坐标是( )
A. (-8,0) B. (0,8)
C. (0,8
 ) D. (0,16)
) D. (0,16) -
科目: 来源: 题型:
查看答案和解析>>【题目】市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
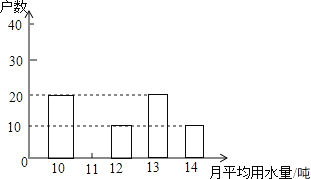
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.

(1)求该抛物线的函数解析式;
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是菱形ABCD的边AB,AD的中点,且AB=5,AC=6.

(1)求对角线BD的长;
(2)求证:四边形AEOF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用大小相同的小三角形摆成如图所示的图案,按照这样的规律摆放,则第n个图案中共有小三角形的个数是 .
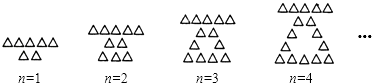
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

相关试题

