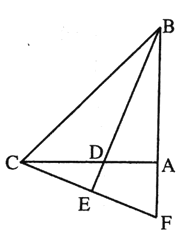
【题目】如图, ![]() 平分
平分![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)证明△ABD≌△ACF即可得到结论;
(2)由(1)得∠ABD=∠ACF,∠CDE=∠BDA,根据三角形内角和定理可得∠CED=∠BAD=90°,即BE⊥CF,结合BD平分∠ABC可证明BC=BF.
(1)∵∠BAC=90°,
∴∠CAF=90°,
∴∠BAC=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠ABD=∠ACF;
(2)在△CDE和△BDA中
∵∠DEC+∠CDE+DCE=180°,∠ABD+∠BDA+∠BAD=180°
又∠ABD=∠ACF,∠CDE=∠BDA,
∴∠CED=∠BDA=90°,
∴∠CEB=∠FEB=90°,
∵BD平分∠ABC
∴∠CBE=∠FBE
又BE为公共边,
∴△CEB≌△FEB,
∴BC=BF.
-
科目: 来源: 题型:
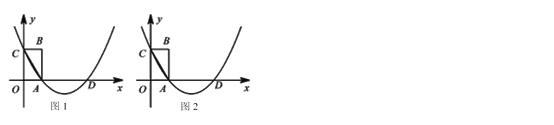
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别位于x轴,y轴上,经过A,C两点的抛物线变x轴于另一点D,连接AC.请你只用无刻度的直尺按要求画图.
(1)在图1中的抛物线上,画出点E,使DE=AC;
(2)在图2中的抛物线上,画出抛物线的顶点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
-
科目: 来源: 题型:
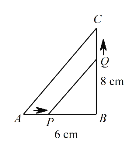
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
(1)如果P,Q分别从A,B两点同时出发,经过几秒钟,△PBQ的面积等于△ABC面积的三分之一?
(2)如果P,Q两点分别从A,B两点同时出发,几秒钟后,P,Q相距6厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电商销售某品牌手表,其成本为每件80元,售价为m元(80<m<240).9月份的销售量为m件,10月份电商对该手表的售价做了调整,在9月份售价的基础上打9折销售,结果销售量增加了50件,销售额增加了5000元.(销售额=销售量×售价)
(1)求该电商9月份销售该品牌手表的销售单价.
(2)11月11日“双十一购物节”,该电商在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=-50x+600.问电商打几折时利润最大,最大利润是多少?
-
科目: 来源: 题型:
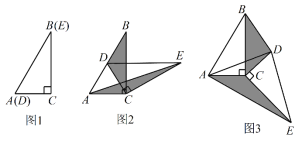
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ;
(2)猜想论证:
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
-
科目: 来源: 题型:
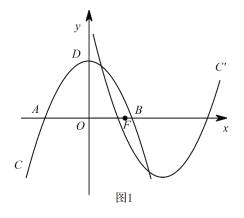
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4
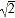 ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
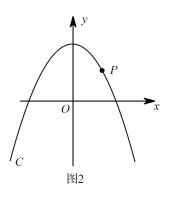
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.
相关试题

