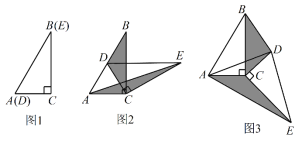
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ;
(2)猜想论证:
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
参考答案:
【答案】(1)DE∥AC;S1=S2;(2)证明见解析.
【解析】
试题(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30角所对的直角边等于斜边的一半求出AC=![]() AB,然后求出AC=BE,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
AB,然后求出AC=BE,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用"角角边"证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
试题解析:
(1)①线段DE与AC的位置关系是 平行 .②S1与S2的数量关系是 相等 .
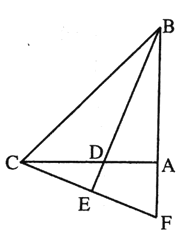
证明:如图2,过D作DN⊥AC交AC于点N,过E作EM⊥AC交AC延长线于M,过C作CF⊥AB交AB于点F.
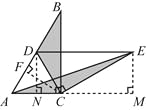
由①可知△ADC是等边三角形,DE∥AC,
∴DN=CF,DN=EM.
∴CF=EM.
∵∠ACB=90,∠B=30,
∴AB=2AC.
又∵AD=AC,
∴BD=AC.
∵S1=![]() CF·BD,S2=
CF·BD,S2=![]() AC·EM,
AC·EM,
∴S1=S2.
证明:如图3,作DG⊥BC于点G,AH⊥CE交EC延长线于点H.

∵∠DCE=∠ACB=90∴∠DCG+∠ACE=180.
又∵∠ACH+∠ACE=180,∴∠ACH=∠DCG.
又∵∠CHA=∠CGD=90,AC=CD,
∴△AHC≌△DGC.
∴AH=DG.
又∵CE=CB,
∴S1=S2.
-
科目: 来源: 题型:
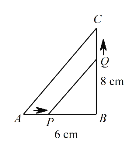
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
(1)如果P,Q分别从A,B两点同时出发,经过几秒钟,△PBQ的面积等于△ABC面积的三分之一?
(2)如果P,Q两点分别从A,B两点同时出发,几秒钟后,P,Q相距6厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平分
平分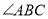 交
交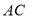 于
于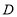 ,交
,交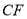 于
于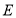 ,
,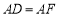 .
.(1)求证:
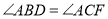 ;
;(2)
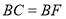 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电商销售某品牌手表,其成本为每件80元,售价为m元(80<m<240).9月份的销售量为m件,10月份电商对该手表的售价做了调整,在9月份售价的基础上打9折销售,结果销售量增加了50件,销售额增加了5000元.(销售额=销售量×售价)
(1)求该电商9月份销售该品牌手表的销售单价.
(2)11月11日“双十一购物节”,该电商在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=-50x+600.问电商打几折时利润最大,最大利润是多少?
-
科目: 来源: 题型:
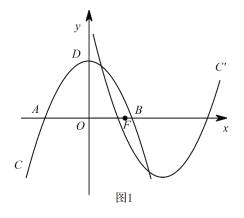
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4
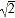 ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
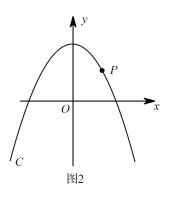
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用3000元购进某种商品,由于销售状况良好,商场又用9000元购进这种商品,但这次的进价比第一次的进价提高了20%,购进商品比第一次的2倍还多300千克,如果商场按每千克9元出售.
求:(1)该种商品第一次的进价是每千克多少元?
(2)超市销售完这种商品共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(-1,0),点B在直线
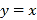 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )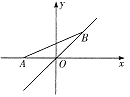
A. (0,0) B. (
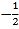 ,
,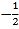 ) C. (
) C. (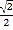 ,
,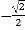 ) D. (
) D. (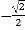 ,
,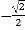 )
)
相关试题

