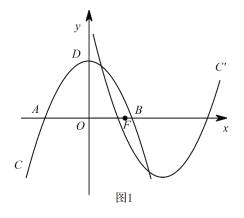
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
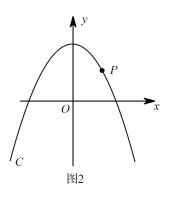
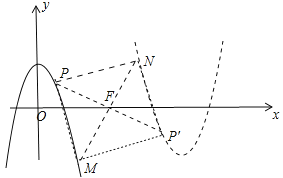
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)2<m<
;(2)2<m<![]() ;(3)m=6或m=
;(3)m=6或m=![]() ﹣3.
﹣3.
【解析】
试题(1)由题意抛物线的顶点C(0,4),A(![]() ,0),设抛物线的解析式为
,0),设抛物线的解析式为![]() ,把A(
,把A(![]() ,0)代入可得a=
,0)代入可得a=![]() ,由此即可解决问题;
,由此即可解决问题;
(2)由题意抛物线C′的顶点坐标为(2m,﹣4),设抛物线C′的解析式为![]() ,由
,由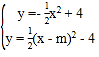 ,消去y得到
,消去y得到![]() ,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有
,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有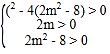 ,解不等式组即可解决问题;
,解不等式组即可解决问题;
(3)情形1,四边形PMP′N能成为正方形.作PE⊥x轴于E,MH⊥x轴于H.由题意易知P(2,2),当△PFM是等腰直角三角形时,四边形PMP′N是正方形,推出PF=FM,∠PFM=90°,易证△PFE≌△FMH,可得PE=FH=2,EF=HM=2﹣m,可得M(m+2,m﹣2),理由待定系数法即可解决问题;情形2,如图,四边形PMP′N是正方形,同法可得M(m﹣2,2﹣m),利用待定系数法即可解决问题.
试题解析:(1)由题意抛物线的顶点C(0,4),A(![]() ,0),设抛物线的解析式为
,0),设抛物线的解析式为![]() ,把A(
,把A(![]() ,0)代入可得a=
,0)代入可得a=![]() ,∴抛物线C的函数表达式为
,∴抛物线C的函数表达式为![]() .
.
(2)由题意抛物线C′的顶点坐标为(2m,﹣4),设抛物线C′的解析式为![]() ,由
,由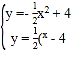 ,消去y得到
,消去y得到![]() ,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有
,由题意,抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,则有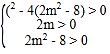 ,解得2<m<
,解得2<m<![]() ,∴满足条件的m的取值范围为2<m<
,∴满足条件的m的取值范围为2<m<![]() .
.
(3)结论:四边形PMP′N能成为正方形.
理由:1情形1,如图,作PE⊥x轴于E,MH⊥x轴于H.

由题意易知P(2,2),当△PFM是等腰直角三角形时,四边形PMP′N是正方形,∴PF=FM,∠PFM=90°,易证△PFE≌△FMH,可得PE=FH=2,EF=HM=2﹣m,∴M(m+2,m﹣2),∵点M在![]() 上,∴
上,∴![]() ,解得m=
,解得m=![]() ﹣3或﹣
﹣3或﹣![]() ﹣3(舍弃),∴m=
﹣3(舍弃),∴m=![]() ﹣3时,四边形PMP′N是正方形.
﹣3时,四边形PMP′N是正方形.
情形2,如图,四边形PMP′N是正方形,同法可得M(m﹣2,2﹣m),把M(m﹣2,2﹣m)代入![]() 中,
中,![]() ,解得m=6或0(舍弃),∴m=6时,四边形PMP′N是正方形.
,解得m=6或0(舍弃),∴m=6时,四边形PMP′N是正方形.
综上所述:m=6或m=![]() ﹣3时,四边形PMP′N是正方形.
﹣3时,四边形PMP′N是正方形.
-
科目: 来源: 题型:
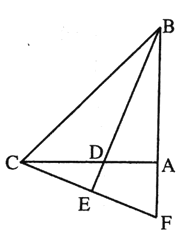
查看答案和解析>>【题目】如图,
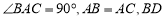 平分
平分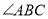 交
交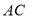 于
于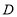 ,交
,交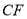 于
于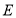 ,
,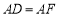 .
.(1)求证:
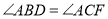 ;
;(2)
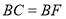 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电商销售某品牌手表,其成本为每件80元,售价为m元(80<m<240).9月份的销售量为m件,10月份电商对该手表的售价做了调整,在9月份售价的基础上打9折销售,结果销售量增加了50件,销售额增加了5000元.(销售额=销售量×售价)
(1)求该电商9月份销售该品牌手表的销售单价.
(2)11月11日“双十一购物节”,该电商在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=-50x+600.问电商打几折时利润最大,最大利润是多少?
-
科目: 来源: 题型:
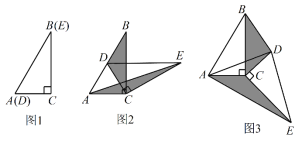
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ;
(2)猜想论证:
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用3000元购进某种商品,由于销售状况良好,商场又用9000元购进这种商品,但这次的进价比第一次的进价提高了20%,购进商品比第一次的2倍还多300千克,如果商场按每千克9元出售.
求:(1)该种商品第一次的进价是每千克多少元?
(2)超市销售完这种商品共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(-1,0),点B在直线
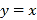 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )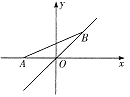
A. (0,0) B. (
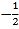 ,
,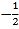 ) C. (
) C. (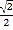 ,
,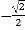 ) D. (
) D. (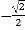 ,
,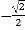 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①
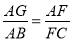 ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=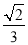 AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若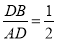 ,则
,则 ,其中正确的结论序号是( )
,其中正确的结论序号是( )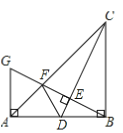
A. ①② B. ③④ C. ①②③ D. ①②③④
相关试题

