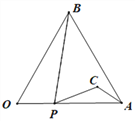
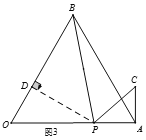
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
参考答案:
【答案】2或![]()
【解析】如图(1)过点P作PD⊥OB于点D,过C作CE⊥OA于E,∴∠PDO=∠PEC=90°,
∵∠O=60°,∴∠OPD=30°,∴OD=![]() t,∴BD=4-
t,∴BD=4-![]() t,PD=
t,PD=![]() t,
t,
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°,BP=2PC,∵∠OPD=30°,
∴∠BPD+∠CPE=90°,∴∠DBP=∠CPE,
∴△PCE∽△BPD,
∴![]() ,
,
∴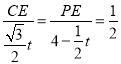 ,
,
∴CE=![]() t,PE=2-
t,PE=2-![]() t,OE=2+
t,OE=2+![]() t,
t,
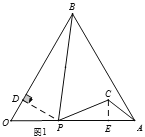
如图(2)当∠PCA=90度时,作CF⊥PA,∴△PCF∽△ACF,∴△PCF∽△ACF,∴![]() ,∴CF2=PFAF,
,∴CF2=PFAF,
∵PF=2-![]() t,AF=4-OF=2-
t,AF=4-OF=2-![]() t, CF=
t, CF=![]() t,
t,
∴(![]() t)2=(2-
t)2=(2-![]() t)(=2-
t)(=2-![]() t),
t),
∴t=2,这时P是OA的中点;
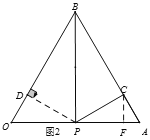
如图(3)当∠CAP=90°时,此时OA=OE,
∴2+![]() t=4,∴t=
t=4,∴t=![]() ,
,
故答案为:2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a﹣b>﹣1;③2a+c<0;④k>a+b;⑤k<﹣1. 其中正确的结论有_________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数
2 -4 8 -16 32 -64 ……
4 -2 10 -24 34 -62 ……
-1 5 -7 17 -31 65 ……
(1)第一行第7个数为
(2)第③行中是否存在连续的三个数使得三个数的和为768?若存在,求出这三个数;不存在,则说明理由;
(3)是否存在这样的一列,使得其中的三个数的和为1282?若存在,则求出这三个数,不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里:
﹣5.
 ,|﹣
,|﹣ |,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1
|,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1 ,23%,﹣π
,23%,﹣π正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
无理数集合:{ }
非负数集合:{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 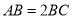 ,
, 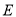 为
为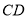 上一点,且
上一点,且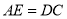 ,
, 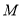 为
为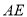 的中点.下列结论:①
的中点.下列结论:①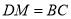 ;②
;②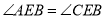 ;③
;③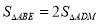 ;④
;④ .其中正确的有____________.(请把所有正确结论的序号填在横线上)
.其中正确的有____________.(请把所有正确结论的序号填在横线上)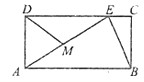
相关试题

