【题目】观察下列三行数
2 -4 8 -16 32 -64 ……
4 -2 10 -24 34 -62 ……
-1 5 -7 17 -31 65 ……
(1)第一行第7个数为
(2)第③行中是否存在连续的三个数使得三个数的和为768?若存在,求出这三个数;不存在,则说明理由;
(3)是否存在这样的一列,使得其中的三个数的和为1282?若存在,则求出这三个数,不存在,则说明理由.
参考答案:
【答案】(1)128;(2)256,-512,1024;(3)分别是521,514,256,使得其中的三个数的和为1282.
【解析】
(1)根据第①行已知数据都是2的乘方得到,再利用第奇数个系数为负数即可得出答案;(2)根据3行数据关系分别分析得出即可;
(3)利用已知规律得出三行数据的规律进而得出方程求出即可.
(1)∵2,-4,8,-16,32,-64,…;
∴21=2,-4=-22,8=23,-16=-24,…
∴第①行第7个数为:27=128;
(2)存在.
设第3个的数和为:(-1)n+1×2n-1+(-1)n+2×2n+(-1)n+3×2n+1=768,
当n为偶数:整理得出:-5×(-2)n-1=768,则求不出整数,
当n为奇数:整理得出:3×2n-1=768,解得:n=9.
这3个数为:256,-512,1024;
(3)存在.
∵同一列的数符号相同,
∴这三个数都是正数,
∴这一列三个数的和为:2n+(2+2n)+![]() ×2n=1282,
×2n=1282,
2n=512,
n=9,
∴存在这样的一列,分别是521,514,256,使得其中的三个数的和为1282.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加了20千米/小时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/小时,请你用学过的知识说明在这条铁路的现有条件下列车是否还可以再提速。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律.例如:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为
 .请利用以上结论解决下列问题.
.请利用以上结论解决下列问题.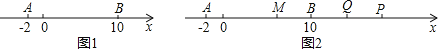
(1)如图1,数轴上点A表示的数为﹣2,点B表示的数为10,则A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
(2)数轴上另有一动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动,点Q是线段BP的中点.设运动时间为t秒:
①当t=2时,求此时点Q表示的数;
②如图2,点P运动至B点右侧,M是线段AQ的中点,若B恰好是QM的中点,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a﹣b>﹣1;③2a+c<0;④k>a+b;⑤k<﹣1. 其中正确的结论有_________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里:
﹣5.
 ,|﹣
,|﹣ |,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1
|,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1 ,23%,﹣π
,23%,﹣π正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
无理数集合:{ }
非负数集合:{ }
-
科目: 来源: 题型:
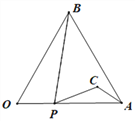
查看答案和解析>>【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

相关试题

