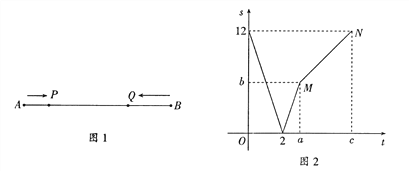
【题目】如图1,线段![]() =12厘米,动点
=12厘米,动点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发向点
出发向点![]()
运动,两点同时出发,到达各自的终点后停止运动.已知动点![]() 运动的速度是动点
运动的速度是动点![]() 运动的速度的2倍.设两点之间的距离为
运动的速度的2倍.设两点之间的距离为![]() (厘米),动点
(厘米),动点![]() 的运动时间为
的运动时间为![]() (秒),图2表示
(秒),图2表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
(1)求动点![]() 、
、![]() 运动的速度;
运动的速度;
(2)图2中, ![]() = ,
= , ![]() = ,
= , ![]() = ;
= ;
(3)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式(即线段
之间的函数关系式(即线段![]() 对应的函数关系式).
对应的函数关系式).
参考答案:
【答案】(1)2cm/s,4cm/s;(2)3,6,6;(3)s=2t(3≤t≤6)
【解析】试题分析:(1)相向而行,利用速度![]() 时间=距离列式.(2)利用(1)的结论,对应图象求解.(3)根据图象中一次函数过定点,利用待定系数求函数解析式.
时间=距离列式.(2)利用(1)的结论,对应图象求解.(3)根据图象中一次函数过定点,利用待定系数求函数解析式.
试题解析:
(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,
根据题意,得2(x+2x)=12,
解得x=2.
答:动点P、Q运动的速度分别是2厘米/秒、4厘米/秒;
(2)动点Q运动的时间a=![]()
经过3秒,动点Q从点B运动到点A,此时动点P运动的路程为2×3=6,即b=6;
动点P运动的时间c=![]()
故答案为3,6,6;
(3)当3≤t≤6时,设s与t之间的函数关系式为s=kt+b,
∵图象过点(3,6),(6,12),∴![]() ,
,
解得![]() ,
,
∴s与t之间的函数关系式为s=2t(3≤t≤6).
-
科目: 来源: 题型:
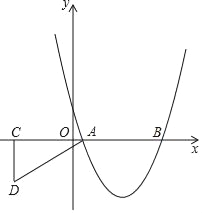
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)过点C(﹣3,0)在x轴下方作x轴的垂线,再以点A为圆心、5为半径长画弧,交先前所作垂线于D,连接AD(如图),将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
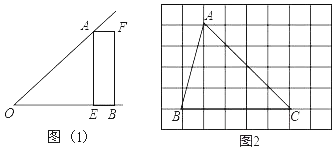
查看答案和解析>>【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法.
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线.
(2)如图2,在8×6的正方形网格中,请用无刻度直尺画一个与△ABC面积相等,且以BC为边的平行四边形,顶点在格点上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
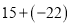 ;
;(2)
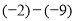 ;
;(3)
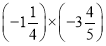
(4)
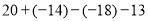 ;
;(5)
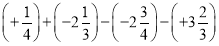
(6)
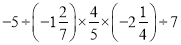 ;
;(7)
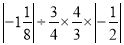
(8)
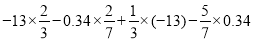
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(1)
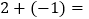 _______;(2)
_______;(2)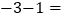 ________;
________;(3)
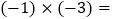 _______;(4)
_______;(4)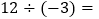 _______;
_______;(5)
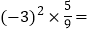 ________;(6)
________;(6)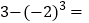 ________.
________. -
科目: 来源: 题型:
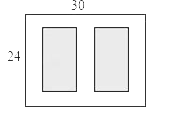
查看答案和解析>>【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间
 用t表示,单位:小时
用t表示,单位:小时 ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按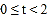 ,
,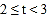 ,
,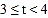 ,
,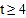 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题: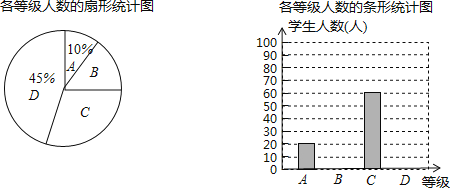
 求本次调查的学生人数;
求本次调查的学生人数; 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整; 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足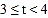 的人数.
的人数.
相关试题

