【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间![]() 用t表示,单位:小时
用t表示,单位:小时![]() ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
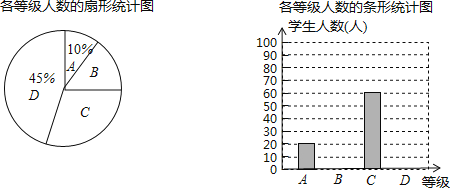
![]() 求本次调查的学生人数;
求本次调查的学生人数;
![]() 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
![]() 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足![]() 的人数.
的人数.
参考答案:
【答案】![]() 本次调查的学生人数为200人;
本次调查的学生人数为200人;![]() B所在扇形的圆心角为
B所在扇形的圆心角为![]() ,补全条形图见解析;
,补全条形图见解析;![]() 全校每周课外阅读时间满足
全校每周课外阅读时间满足![]() 的约有360人.
的约有360人.
【解析】![]() 根据等级A的人数及所占百分比即可得出调查学生人数;
根据等级A的人数及所占百分比即可得出调查学生人数;
![]() 先计算出C在扇形图中的百分比,用
先计算出C在扇形图中的百分比,用![]() 在扇形图中的百分比
在扇形图中的百分比![]() 可计算出B在扇形图中的百分比,再计算出B在扇形的圆心角;
可计算出B在扇形图中的百分比,再计算出B在扇形的圆心角;
![]() 总人数
总人数![]() 课外阅读时间满足
课外阅读时间满足![]() 的百分比即得所求.
的百分比即得所求.
![]() 由条形图知,A级的人数为20人,
由条形图知,A级的人数为20人,
由扇形图知:A级人数占总调查人数的![]() ,
,
所以:![]() 人
人![]() ,
,
即本次调查的学生人数为200人;
![]() 由条形图知:C级的人数为60人,
由条形图知:C级的人数为60人,
所以C级所占的百分比为:![]() ,
,
B级所占的百分比为:![]() ,
,
B级的人数为![]() 人
人![]() ,
,
D级的人数为:![]() 人
人![]() ,
,
B所在扇形的圆心角为:![]() ,
,
补全条形图如图所示:
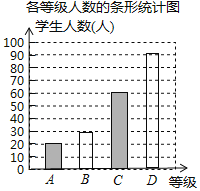 ;
;
![]() 因为C级所占的百分比为
因为C级所占的百分比为![]() ,
,
所以全校每周课外阅读时间满足![]() 的人数为:
的人数为:![]() 人
人![]() ,
,
答:全校每周课外阅读时间满足![]() 的约有360人.
的约有360人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,线段
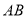 =12厘米,动点
=12厘米,动点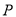 从点
从点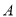 出发向点
出发向点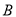 运动,动点
运动,动点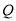 从点
从点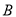 出发向点
出发向点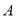
运动,两点同时出发,到达各自的终点后停止运动.已知动点
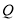 运动的速度是动点
运动的速度是动点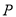 运动的速度的2倍.设两点之间的距离为
运动的速度的2倍.设两点之间的距离为 (厘米),动点
(厘米),动点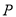 的运动时间为
的运动时间为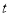 (秒),图2表示
(秒),图2表示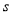 与
与 之间的函数关系.
之间的函数关系.(1)求动点
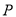 、
、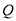 运动的速度;
运动的速度;(2)图2中,
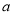 = ,
= , 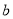 = ,
= , 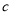 = ;
= ;(3)当
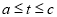 时,求
时,求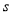 与
与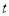 之间的函数关系式(即线段
之间的函数关系式(即线段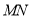 对应的函数关系式).
对应的函数关系式).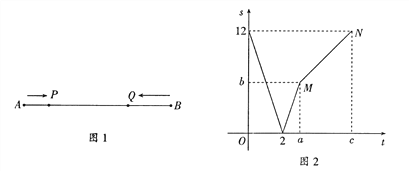
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(1)
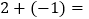 _______;(2)
_______;(2)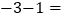 ________;
________;(3)
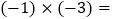 _______;(4)
_______;(4)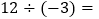 _______;
_______;(5)
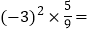 ________;(6)
________;(6)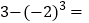 ________.
________. -
科目: 来源: 题型:
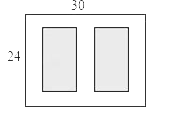
查看答案和解析>>【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个三角形的两条边和其中一边上的高对应相等,那么这两个三角形的第三边所对的角的关系是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
相关试题

