【题目】如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 . 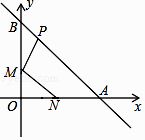
参考答案:
【答案】![]()
【解析】解:如图,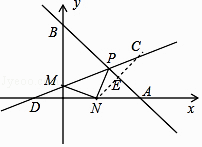
点N关于OB的对称点D(﹣1,0),点N关于直线AB的对称点C,
∵直线AB的解析式为y=﹣x+2,
∴直线NC的解析式为y=x﹣1,
由 ![]() 解得
解得 ![]() ,
,
∴E( ![]() ,
, ![]() ),
),
∵E是NC中点,
∴可得C(4,1).
连接DC与BO交于点M,与AB交于点P,此时PM+MN最小,
∴直线CD的解析式为:y= ![]() x+
x+ ![]() ,
,
由 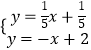 解得:
解得: ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
∴PM+MN=PD= ![]() =
= ![]() .
.
∴PM+MN的最小值是 ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的一次函数的性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数
图形
最多剪出的小三角形个数
1
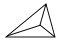
3
2
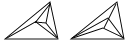
5
3
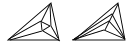
7
…
…
…
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当x≠1时,a+b>ax2+bx;④a﹣b+c>0.
其中正确的有 .
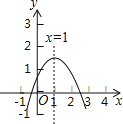
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的周长是12,那么这个正六边形的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,求B、C两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小文同学每天乘从BRT(城市快速公交)上学,为了方便乘坐BRT,他用自己勤工俭学的钱买了80元的公交卡.如果他乘坐的次数用n表示,则记录他每次乘坐BRT后公交卡的余额(单位:元)如下表:
次数n
余额(元)
1
80-0.9
2
80-1.8
3
80-2.7
4
80-3.6
…
…
(1)写出用乘坐BRT的次数n表示余额的式子为____________________;
(2)利用(1)中的式子,帮助小文同学算一算,他一个月乘坐BRT有84次,这80元的公交卡够不够用,若够用,能剩多少元?
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: ﹣(3﹣π)0﹣|﹣3+2|;
﹣(3﹣π)0﹣|﹣3+2|;
(2)计算: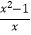 ÷(1+
÷(1+  )
)
相关试题

