【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数 | 图形 | 最多剪出的小三角形个数 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
参考答案:
【答案】(1)9;(2)2;(3)2n+1;(4)n2+2n+1.
【解析】
(1)利用表格中数据得出三角形个数的变化可推出n=4时,最多剪得的三角形的个数;
(2)利用(1)中数据得出三角形个数的变化规律即可;
(3)利用(2)中变化规律即可得出当三角形内点的个数为n时,最多可以剪得三角形的个数;
问题拓展:利用补项法求出答案.
(1)∵当三角形内点的个数为1时,最多可以剪得3个三角形;
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
∴当三角形内点的个数为4时,最多可以剪得9个三角形;
故答案为:9;
(2)由(1)的结果可得出:三角形内的点每增加1个,最多剪得的三角形增加2个;
故答案为:2;
(3)∵1×2+1=3,2×2+1=5,3×2+1=7,
∴当三角形内点的个数为n时,最多可以剪得(2n+1)个三角形;
故答案为:2n+1;
【问题拓展】
1+3+5+7+…+(2n-1)+(2n+1)
=![]() [1+3+5+7+…+(2n-1)+(2n+1)][(2n+1)+(2n-1)+…+7+5+3+1]
[1+3+5+7+…+(2n-1)+(2n+1)][(2n+1)+(2n-1)+…+7+5+3+1]
=![]() (n+1)(1+2n+1)
(n+1)(1+2n+1)
=(n+1)2
=n2+2n+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)第一届现代奥运会于1896年在希腊雅典举行,此后每4年举行一次,奥运会如因故不能举行,届数照算.则奥运会的年份可排成如下一列数:
1896,1900,1904,1908,…
观察上面一列数,我们发现这一列数从第二项起,每一项与它前一项的差都等于同一个常数4,这一列数在数学上叫做等差数列,这个常数4叫做等差数列的公差.
(1)等差数列2,5,8,…的第五项多少;
(2)若一个等差数列的第二项是28,第三项是46,则它的公差为多少,第一项为多少,第五项为多少;
(3)聪明的小雪同学作了一些思考,如果一列数a1,a2,a3,…是等差数列,且公差为d,根据上述规定,应该有:
a 2-a1=d,a3-a2= d,a4-a3= d,…
所以a 2=a1+d,
a3=a2+d=(a1+d)+d=a1+2d,
a4=a3+d=( a1+2d)+d=a1+3d,
…
则等差数列的第n项an多少 (用含有a1、n与d的代数式表示);
(4)按照上面的推理,2008年中国北京奥运会是第几届奥运会,2050年会不会(填“会”或“不会”)举行奥运会.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
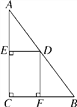
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=kx+b与反比例函数y=
 的图像如图所示,则关于x的不等式kx+b﹣
的图像如图所示,则关于x的不等式kx+b﹣  ≤﹣2的解集为( )
≤﹣2的解集为( ) 
A.0<x≤2或x≤﹣4
B.﹣4≤x<0或x≥2
C. ≤x<0或x
≤x<0或x 
D.x 或0
或0 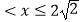
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当x≠1时,a+b>ax2+bx;④a﹣b+c>0.
其中正确的有 .
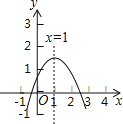
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的周长是12,那么这个正六边形的面积是 .
-
科目: 来源: 题型:
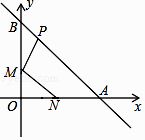
查看答案和解析>>【题目】如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 .
相关试题

