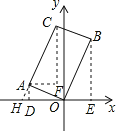
【题目】如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,求B、C两点的坐标.

参考答案:
【答案】点C的坐标为![]() .
.
【解析】首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.
过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
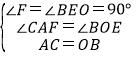 ,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4-1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴![]() ,
,
即![]() ,
,
∴OE=![]() ,
,
即点B(![]() ,3),
,3),
∴AF=OE=![]() ,
,
∴点C的横坐标为:-(2-![]() )=-
)=-![]() ,
,
∴点C(-![]() ,4).
,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当x≠1时,a+b>ax2+bx;④a﹣b+c>0.
其中正确的有 .
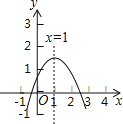
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的周长是12,那么这个正六边形的面积是 .
-
科目: 来源: 题型:
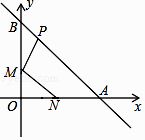
查看答案和解析>>【题目】如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小文同学每天乘从BRT(城市快速公交)上学,为了方便乘坐BRT,他用自己勤工俭学的钱买了80元的公交卡.如果他乘坐的次数用n表示,则记录他每次乘坐BRT后公交卡的余额(单位:元)如下表:
次数n
余额(元)
1
80-0.9
2
80-1.8
3
80-2.7
4
80-3.6
…
…
(1)写出用乘坐BRT的次数n表示余额的式子为____________________;
(2)利用(1)中的式子,帮助小文同学算一算,他一个月乘坐BRT有84次,这80元的公交卡够不够用,若够用,能剩多少元?
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: ﹣(3﹣π)0﹣|﹣3+2|;
﹣(3﹣π)0﹣|﹣3+2|;
(2)计算: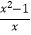 ÷(1+
÷(1+  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
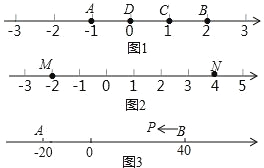
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
相关试题

