【题目】某中学八年级(1)班去体育用品商店买一些篮球和排球,供班上同学阳光体育课间使用,共买了3个篮球和5个排球,花570元,并且每个排球比篮球便宜30元.
(1)求篮球和排球的单价各是多少吗?
(2)商店里搞活动,有两种套餐,①套装打折:五个篮球和五个排球为一套装,套装打八折;②满减活动:999减100,1999减200;两种活动不重复参与,学校打算买15个篮球,13个排球作为奖品,请问如何安排更划算?
参考答案:
【答案】(1) 篮球的单价是90元,排球的单价为60元 ;(2) 照套装①购买更划算
【解析】
(1)设篮球的单价是x元,排球的单价为y元,根据题目中的等量关系列出方程组求解即可;
(2)根据题意中的等量关系列出等式分别求出两个套装需要付款的总数,比较大小即可.
解:(1)设篮球的单价是x元,排球的单价为y元,
根据题意得:
![]() ,
,
解得:
![]() ,
,
答:篮球的单价是90元,排球的单价为60元;
(2)按照套装①打折,
买15个篮球和15个排球需付款:15×90×0.8+15×60×0.8=1800(元),
按照套装②打折,
15个篮球需付款:15×90=1350(元),
13个排球需付款:13×60=780(元),
共需付款:1350+780﹣200=1930(元),
即按照套装①购买更划算,
答:按照套装①购买更划算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.

(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】图甲是任意一个直角三角形ABC,它的两条直角边的长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
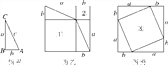
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②面积之和为__________;
(4)图乙中①②的面积之和与图丙中正方形③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
-
科目: 来源: 题型:
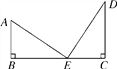
查看答案和解析>>【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A. ﹣
﹣  =
= 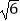
B.| ﹣2|=﹣
﹣2|=﹣ 
C. =2
=2 
D.( )﹣1=2
)﹣1=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B若干次(每次A、B两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品A、B同时打折.三次购买商品A、B的数量和费用如表所示.
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
980
第二次购物
3
7
940
第三次购物
9
8
912
(1)求商品A、B的标价;
(2)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购物共花去了960元,则小林有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求值问题中,我们经常遇到利用整体思想来解决问题.
例如1:已知:x+2y﹣3z=2,2x+y+6z=1,求:x+y+z的值
解:令x+2y﹣3z=2﹣﹣﹣﹣﹣①2x+y+6z=1﹣﹣﹣﹣﹣﹣②
①+②得3x+3y+3z=3所以x+y+z=1
已知
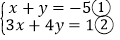 求x+2y的值
求x+2y的值解:①×2得:2x+2y=﹣10③
②﹣③得:x+2y=11
利用材料中提供的方法,解决下列问题
(1)已知:关于x,y的二元一次方程组
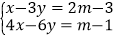 的解满足x﹣y=6,求m的值
的解满足x﹣y=6,求m的值(2)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙咱盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
相关试题

