【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:当k=1时,抛物线解析式为y=x2﹣1,直线解析式为y=x+1.
联立两个解析式,得:x2﹣1=x+1,
解得:x=﹣1或x=2,
当x=﹣1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(﹣1,0),B(2,3)
(2)
解:方法一:设P(x,x2﹣1).
如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).
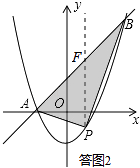
∴PF=yF﹣yP=(x+1)﹣(x2﹣1)=﹣x2+x+2.
S△ABP=S△PFA+S△PFB= ![]() PF(xF﹣xA)+
PF(xF﹣xA)+ ![]() PF(xB﹣xF)=
PF(xB﹣xF)= ![]() PF(xB﹣xA)=
PF(xB﹣xA)= ![]() PF
PF
∴S△ABP= ![]() (﹣x2+x+2)=﹣
(﹣x2+x+2)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]()
当x= ![]() 时,yP=x2﹣1=﹣
时,yP=x2﹣1=﹣ ![]() .
.
∴△ABP面积最大值为 ![]() ,此时点P坐标为(
,此时点P坐标为( ![]() ,﹣
,﹣ ![]() )
)
方法二:过点P作x轴垂线,交直线AB于F,

设P(t,t2﹣1),则F(t,t+1)
∴S△ABP= ![]() (FY﹣PY)(BX﹣AX),
(FY﹣PY)(BX﹣AX),
∴S△ABP= ![]() (t+1﹣t2+1)(2+1),
(t+1﹣t2+1)(2+1),
∴S△ABP=﹣ ![]() t2+
t2+ ![]() t+3,
t+3,
当t= ![]() 时,S△ABP有最大值,∴S△ABP=
时,S△ABP有最大值,∴S△ABP= ![]()
(3)
解:方法一:设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(﹣ ![]() ,0),F(0,1),OE=
,0),F(0,1),OE= ![]() ,OF=1.
,OF=1.
在Rt△EOF中,由勾股定理得:EF= ![]() =
= ![]() .
.
令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1.
∴C(﹣k,0),OC=k.
Ⅰ、假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,
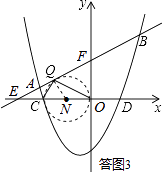
则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.
设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON= ![]() .
.
∴EN=OE﹣ON= ![]() ﹣
﹣ ![]() .
.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,
∴△EQN∽△EOF,
∴ ![]() ,即:
,即: 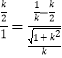 ,
,
解得:k=± ![]() ,
,
∵k>0,
∴k= ![]() .
.
∴存在唯一一点Q,使得∠OQC=90°,此时k= ![]() .
.
Ⅱ、若直线AB过点C时,此时直线与圆的交点只有另一点Q点,故亦存在唯一一点Q,使得∠OQC=90°,
将C(﹣k,0)代入y=kx+1中,
可得k=1,k=﹣1(舍去),
故存在唯一一点Q,使得∠OQC=90°,此时k=1.
综上所述,k= ![]() 或1时,存在唯一一点Q,使得∠OQC=90°
或1时,存在唯一一点Q,使得∠OQC=90°
方法二:∵y=x2+(k﹣1)x﹣k,
∴y=(x+k)(x﹣1),
当y=0时,x1=﹣k,x2=1,
∴C(﹣k,0),D(1,0),
点Q在y=kx+1上,设Q(t,kt+1),O(0,0),
∵∠OQC=90°,∴CQ⊥OQ,∴KCQ×KOQ=﹣1,
∴ ![]() <
<
∴(k2+1)t2+3kt+1=0有唯一解,
∴△=(3k)2﹣4(k2+1)=0,
∴k1= ![]() ,k2=﹣
,k2=﹣ ![]() (k>0故舍去),∴k=
(k>0故舍去),∴k= ![]()
【解析】方法一:(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;(3)“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与抛物线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.方法二:(1)联立直线与抛物线方程求出点A,B坐标.(2)利用面积公式求出P点坐标.(3)列出定点O坐标,用参数表示C,Q点坐标,利用黄金法则二求出k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每个每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是( )
A. 3分钟 B. 3.75分钟 C. 4分钟 D. 5分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造OACD,设点P的横坐标为m.

(1)求直线AB的函数表达式;
(2)若四边形OACD恰是菱形,请求出m的值;
(3)在(2)的条件下,y轴的正半轴上是否存在点Q,连结CQ,使得∠OQC+∠ODC=180°.若存在,直接写出所有符合条件的点Q的坐标,若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】图甲是任意一个直角三角形ABC,它的两条直角边的长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
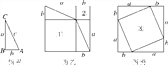
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②面积之和为__________;
(4)图乙中①②的面积之和与图丙中正方形③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
-
科目: 来源: 题型:
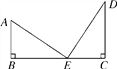
查看答案和解析>>【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级(1)班去体育用品商店买一些篮球和排球,供班上同学阳光体育课间使用,共买了3个篮球和5个排球,花570元,并且每个排球比篮球便宜30元.
(1)求篮球和排球的单价各是多少吗?
(2)商店里搞活动,有两种套餐,①套装打折:五个篮球和五个排球为一套装,套装打八折;②满减活动:999减100,1999减200;两种活动不重复参与,学校打算买15个篮球,13个排球作为奖品,请问如何安排更划算?
相关试题

