【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,﹣1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.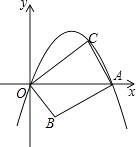
(1)求点A的横坐标.(用含m的代数式表示).
(2)若m=3,则点C的坐标为 .
(3)当点C与抛物线的顶点重合时,求四边形ABOC的面积.
(4)结合m的取值范围,直接写出∠AOC的度数.
参考答案:
【答案】
(1)
解:∵抛物线y=﹣x2+mx与x轴交于点A,
∴﹣x2+mx=0,解得x=0或m,
∴点A的横坐标为m.
(2)(2,2)
(3)
解:如图2中,作BD⊥OA于D,CE⊥OA于E.

由(2)可知△ADB≌△CEA,
∴BD=AE,AD=CE
∵B(1,﹣1),A(m,0),
∴OE=m﹣1,CE=m﹣1,
∴C(m﹣1,m﹣1),
∵点C(m﹣1,m﹣1)与抛物线的顶点( ![]() ,
, ![]() )重合,
)重合,
∴m﹣1= ![]() ,
,
∴m=2.
∴S四边形ABOC= ![]() ×2×(1+1)=2.
×2×(1+1)=2.
(4)
解:①如图3中,当O<m<1时,∠AOC=135°,理由如下:
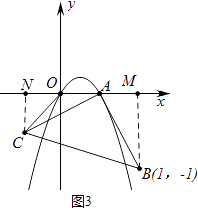
作CN⊥x轴于N,BM⊥x轴于M.
∵∠NAC+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠NAC=∠ABM,
在△ACN和△BAM中,
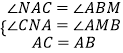 ,
,
∴△ACN≌△BAM,
∴BM=AN=1,CN=AM,
∴AN=OM=1,
∴ON=CN,
∴∠NOC=∠NC0=45°,
∴∠AOC=135°
②当m>1时,∠AOC=45°,理由如下:
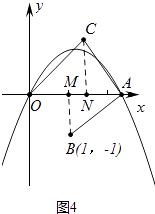
作CN⊥x轴于N,BM⊥x轴于M,∵△ACN≌△BAM,
∴BM=AN=OM=1,AM=CN,
∴ON=AM=CN,∵∠ONC=90°,
∴∠COA=45°.
【解析】解:(2)如图1中,∵m=3,
∴点A坐标为(3,0),
作BD⊥OA于D,CE⊥OA于E.
∵∠ADB=∠AEC=∠BAC=90°,
∴∠DAB+∠DBA=90°,∠DAB+∠CAE=90°,
∴∠CAE=∠DBA,
在△ADB和△CEA中, ,
,
∴△ADB≌△CEA,
∴BD=AE=1,AD=CE=2,
∴点C坐标(2,2).
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有( )

A. 一处 B. 二处 C. 三处 D. 四处
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
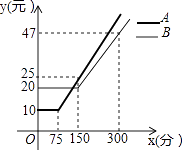
(1)当手机通话时间为50分钟时,写出A、B两种套餐的通话费用.
(2)求a,b的值.
(3)当选择B种套餐比A种套餐更合算时,求通话时间x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.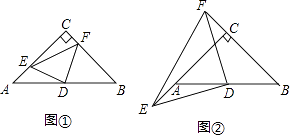
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

相关试题

